
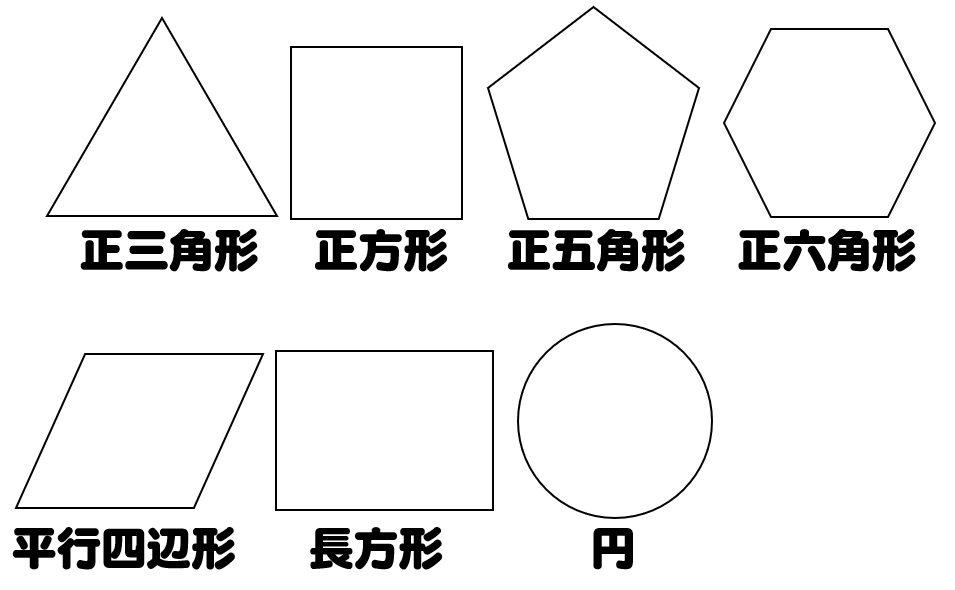
6年算数対称な図形2 正多角形教え方
①、点の「X軸対称」のやり方がわかる ②、点の「Y軸対称」のやり方がわかる ③、点の「原点対称」のやり方がわかる というメリットがあるわけですね 数学おじさん その通りじゃ では解説をはじめるかのぉ 目次 1 数学点の「対称移動(たいしょういどう)ってどうやるの?高校数 2次元ベクトル空間上における点A (6,4) を(1),(2)の方法で移動させた点の座標を求めなさい。 (1) 原点中心に \( 30^{\circ} \) 回転させた点Bの座標 (2) 直線 \( y = 2x \) について対称移動させた点Cの座標 5.練習問題の答え 解答1 (1) \( x \) 軸に関する対称移動 正解:①
線対称 点対称 問題
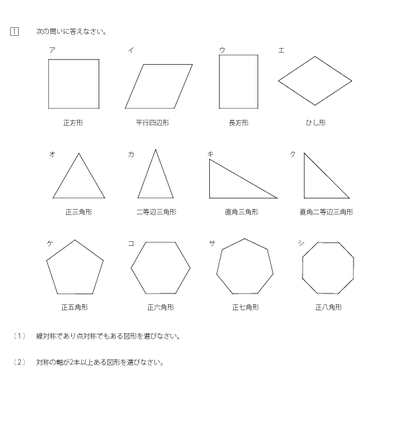
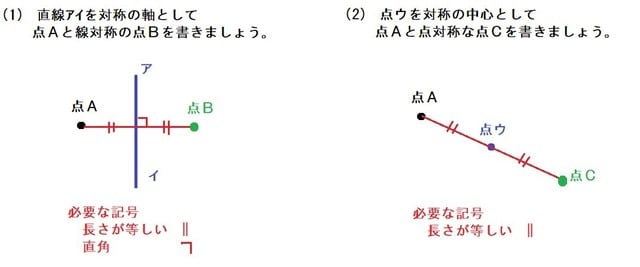
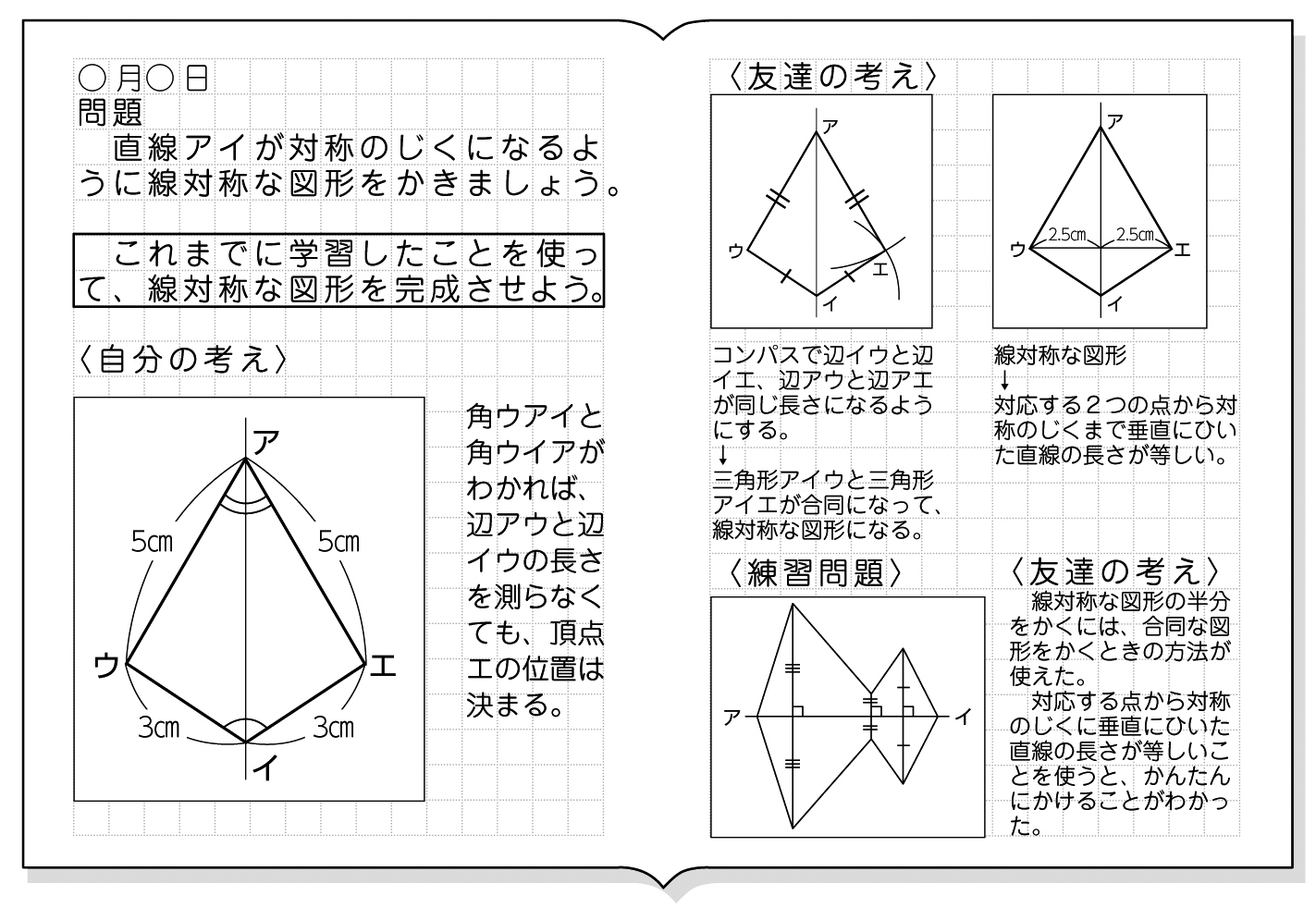
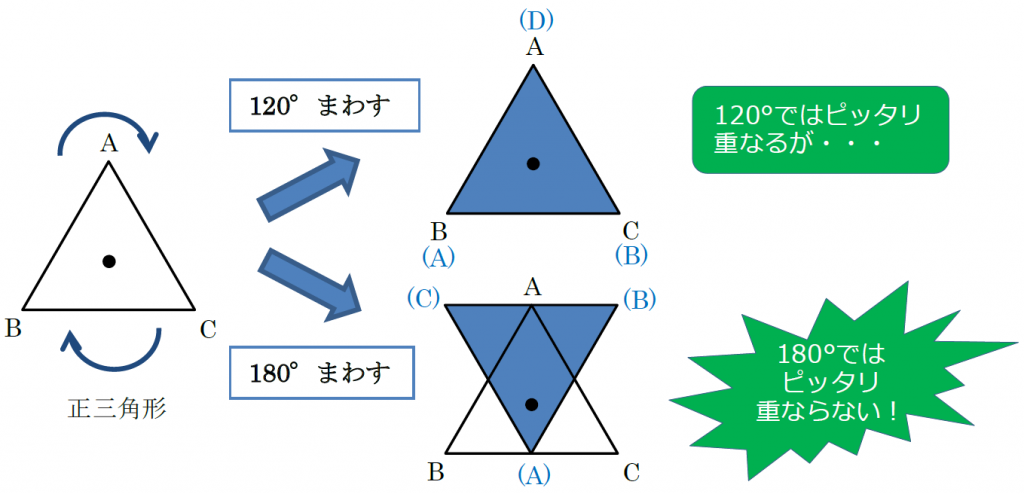
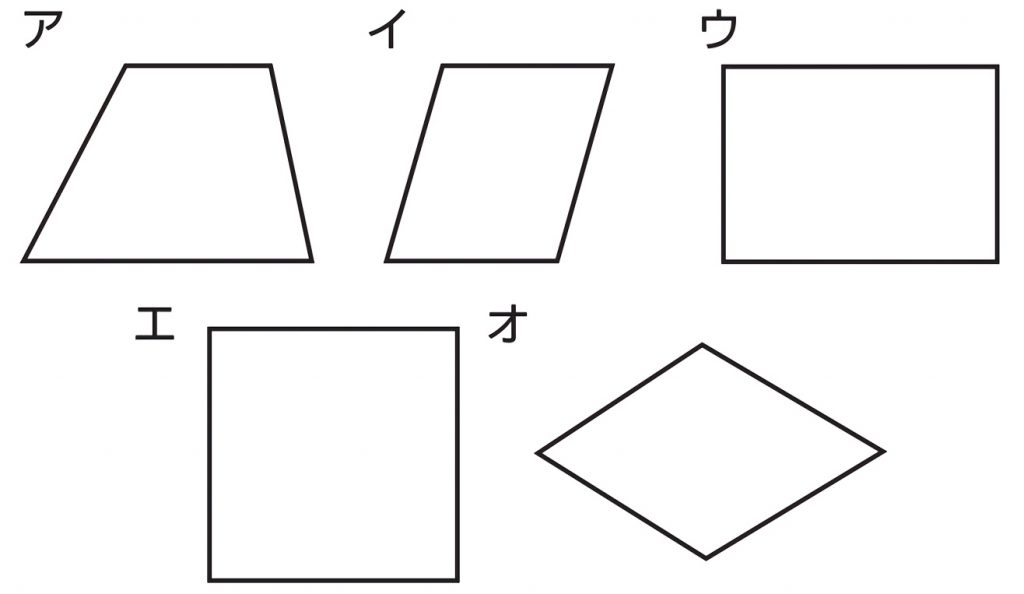
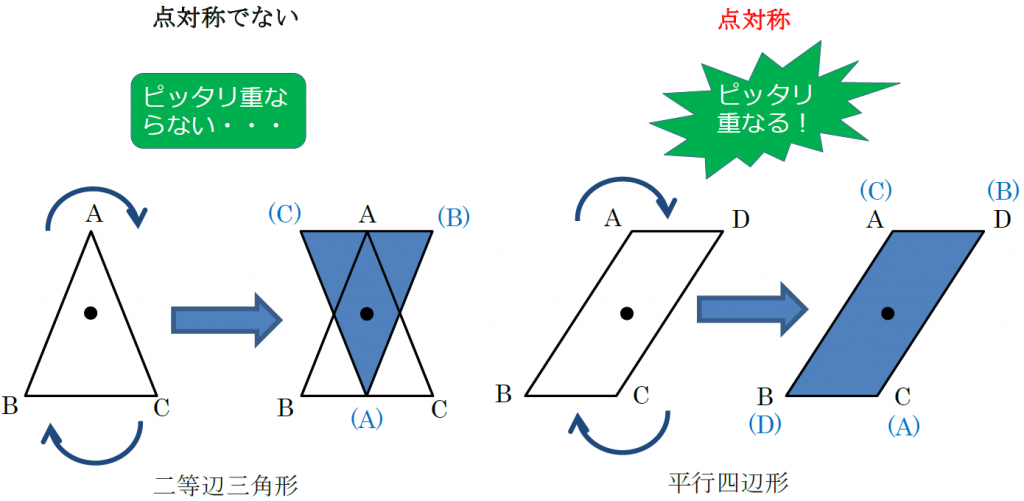
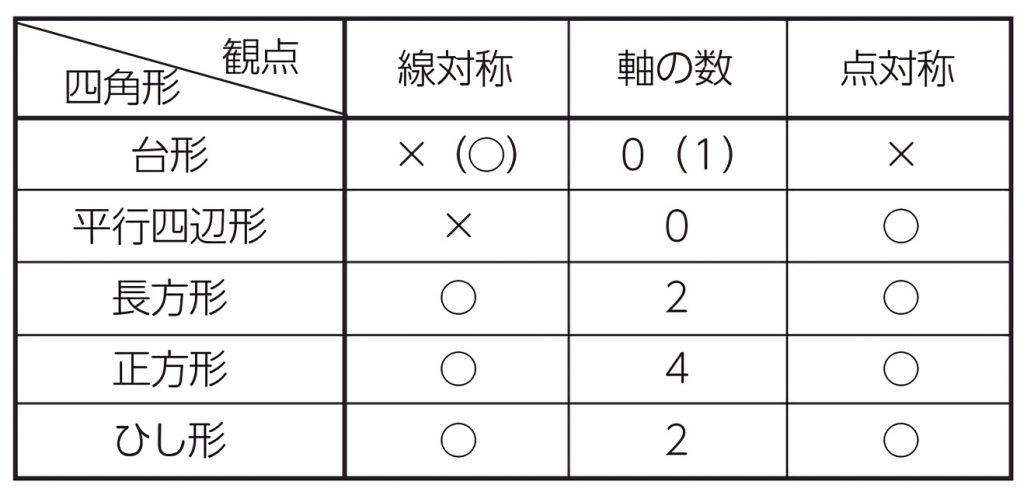
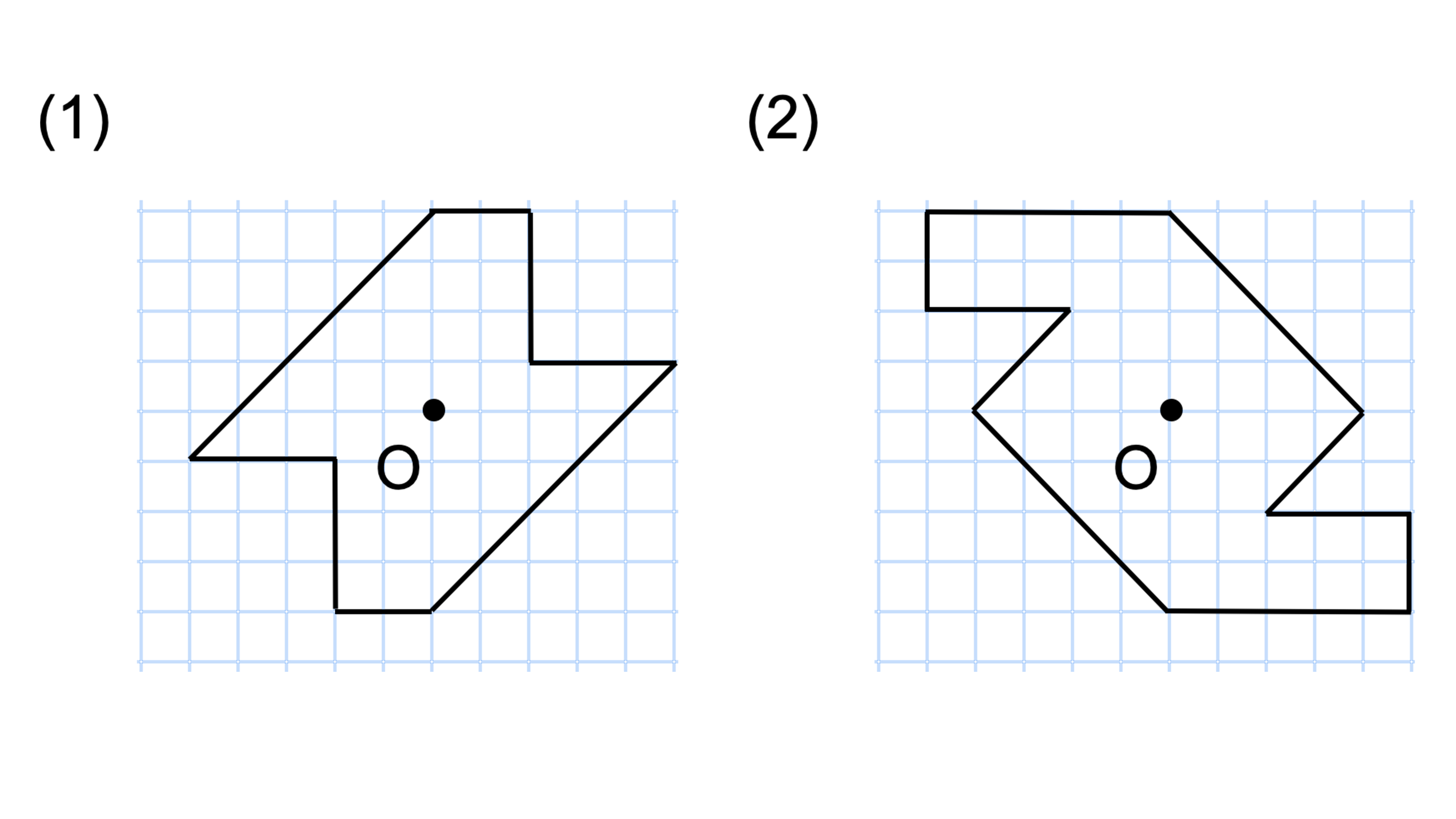
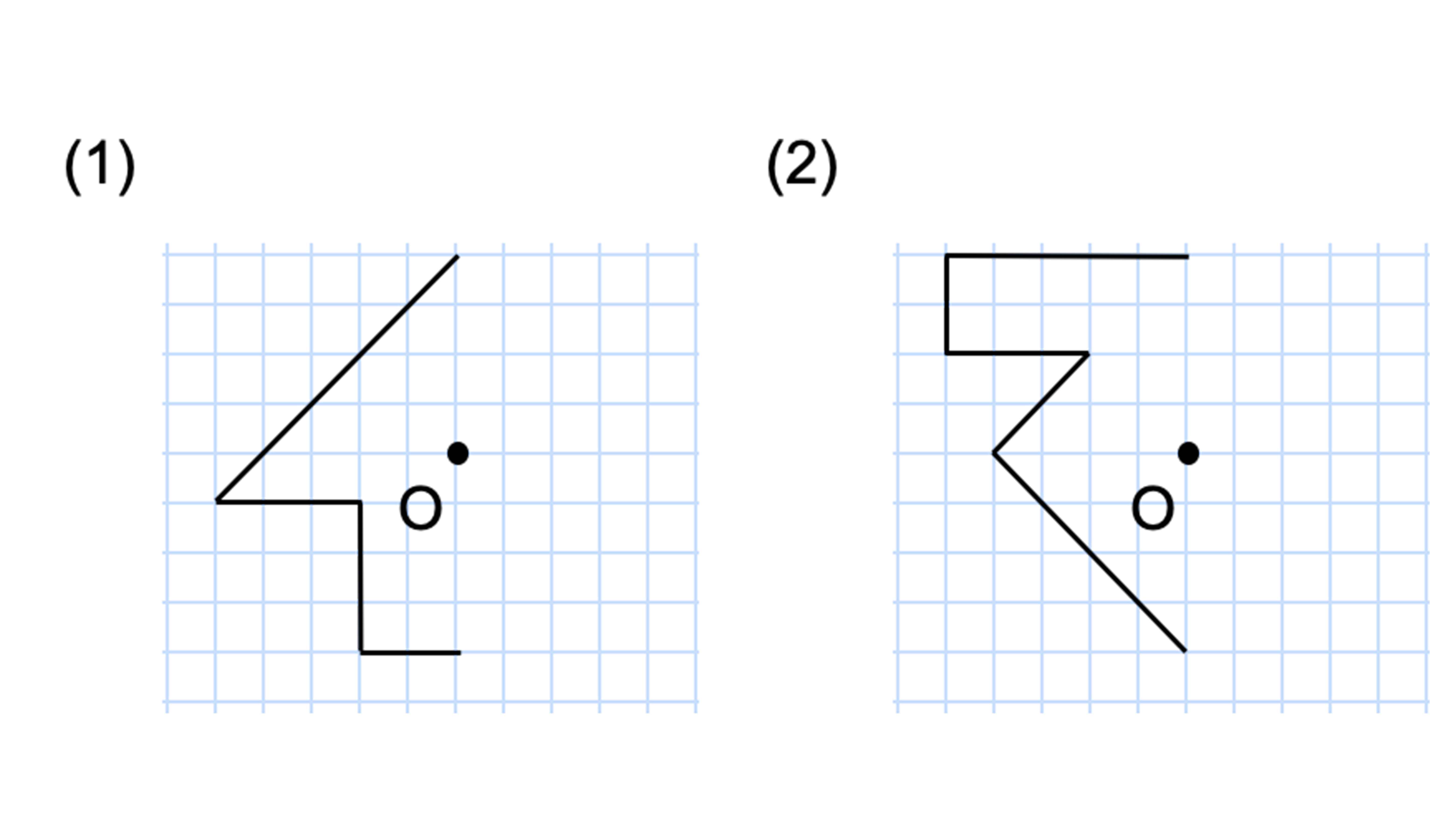
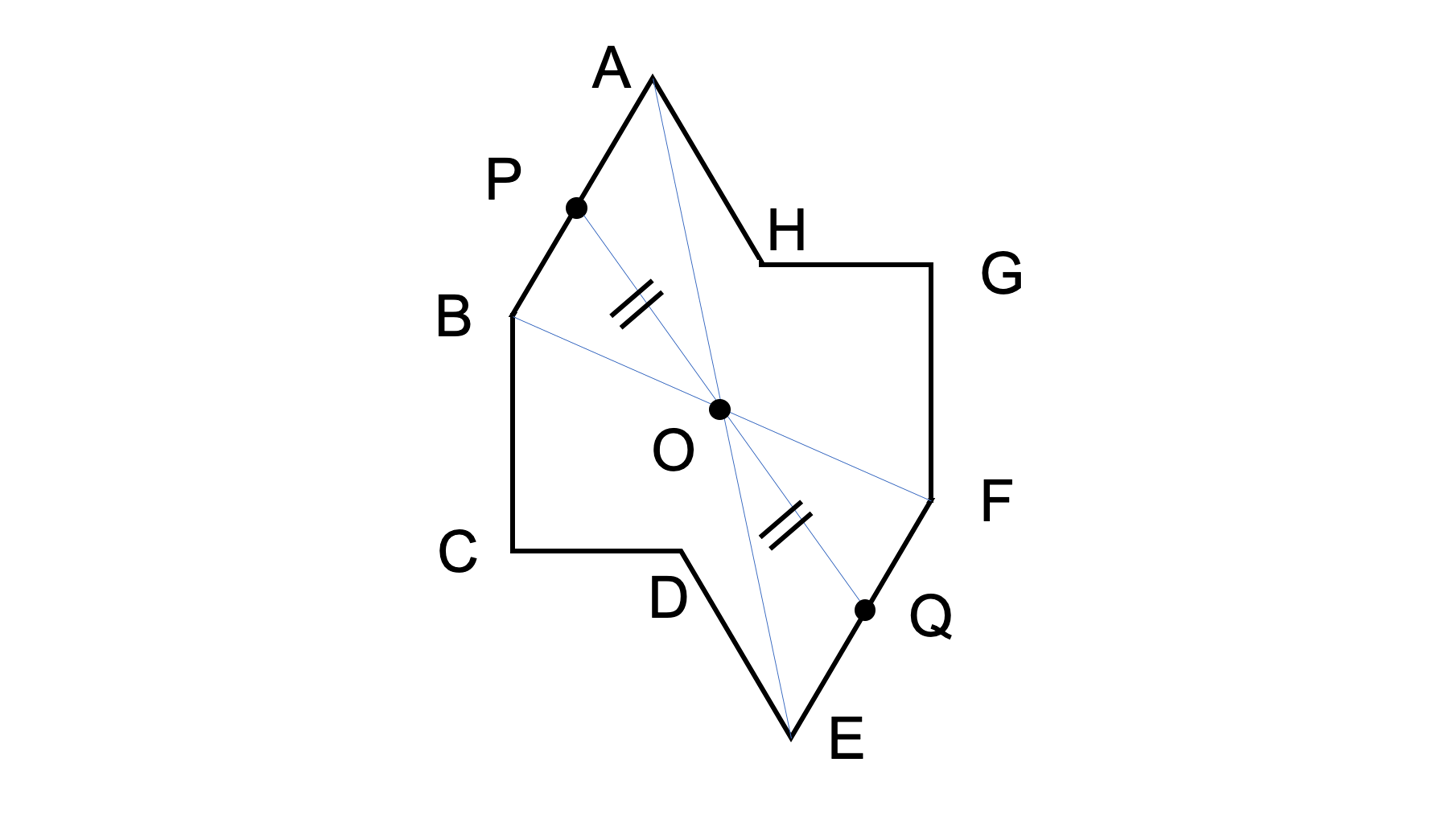
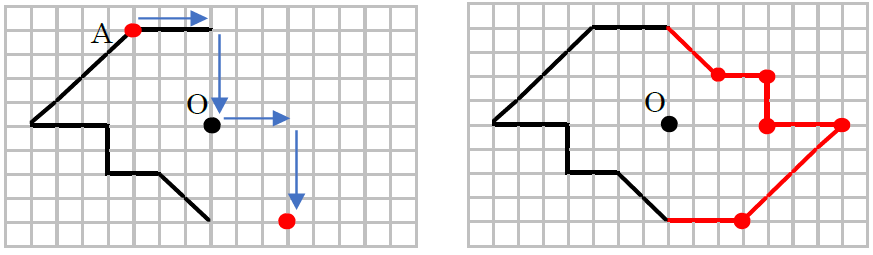
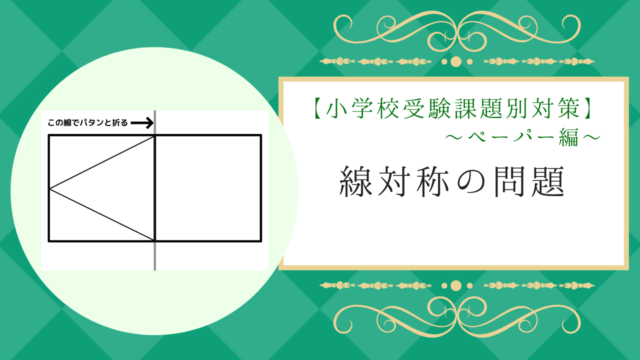
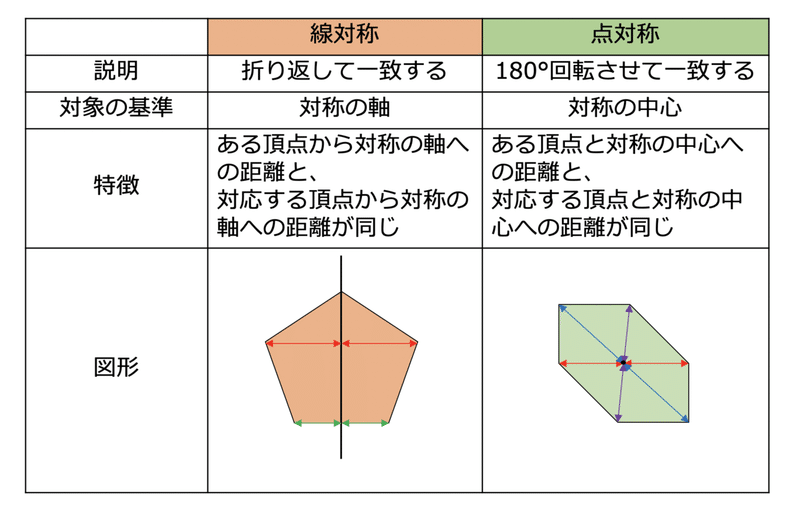
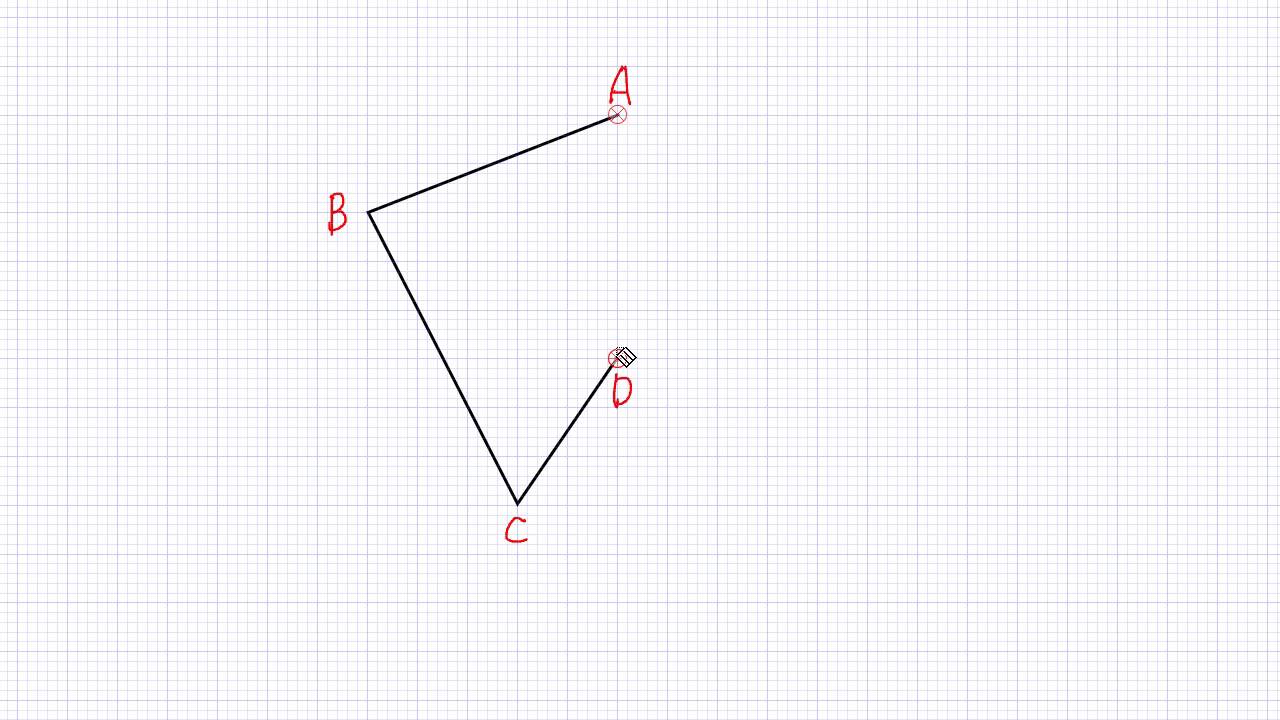
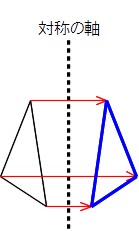
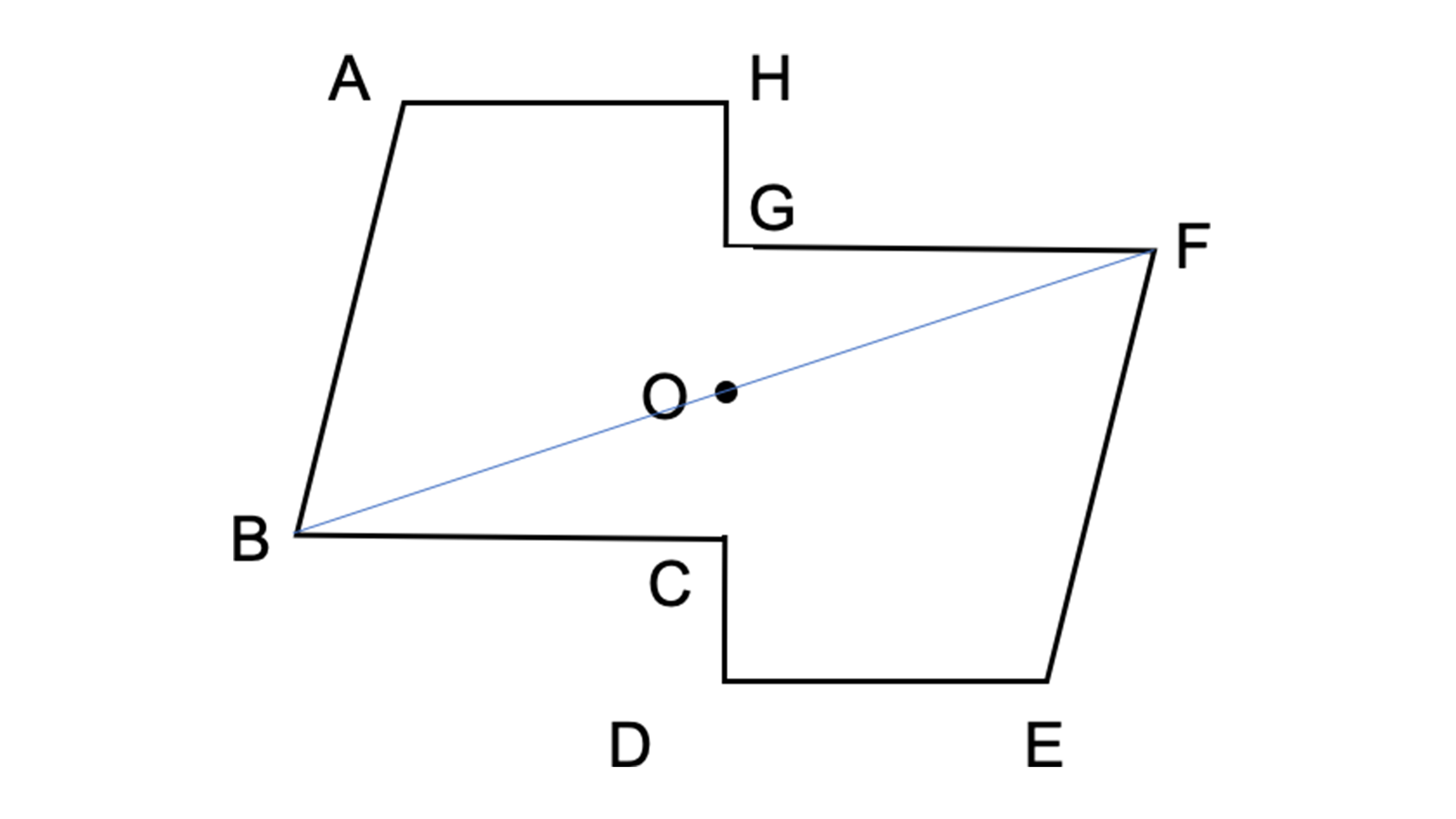
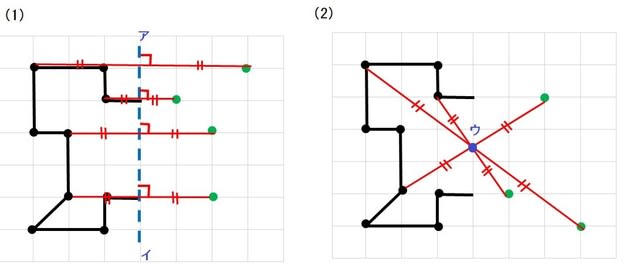
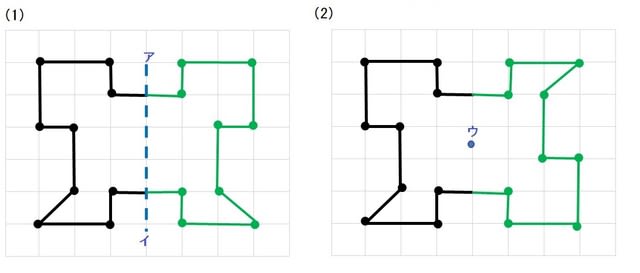
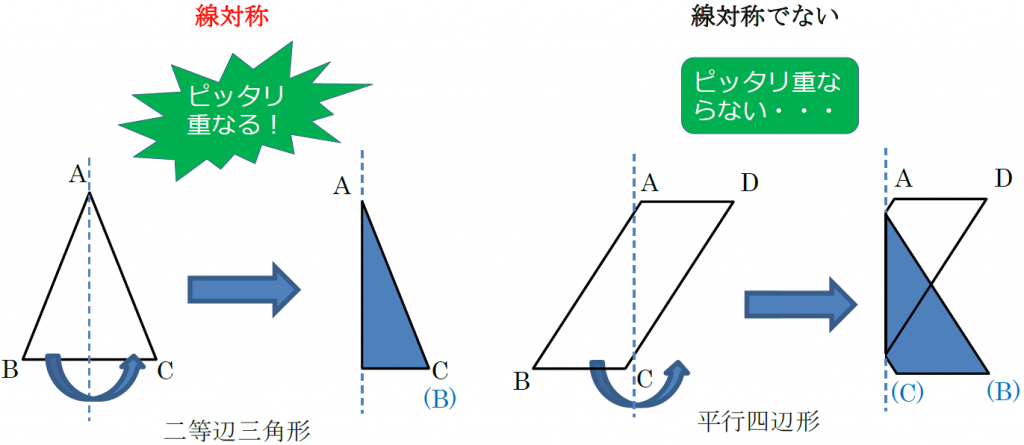
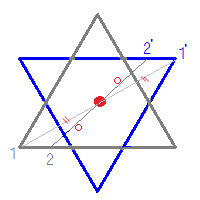
線対称 点対称 問題- 評価問題 たこ形の図形は線対称でしょうか、点対称でしょうか。理由も説明しましょう。 子供に期待する解答の具体例 この線で折ると、ぴったり重なる。 対称の軸があるので、線対称な図形です。 180°回転しても重ならない。 対称の中心がないので点対称ではありません。 本時の評価規 線対称の作図のやり方 aとa'を結んだ直線が対称の軸と垂直に交わって、その交点で二等分されるように点をひいていく。他の点も同じように作図する。 *定規やコンパスで作図してみましょう。 *点対称の場合は180°の回転移動と考えて作図してください。
線対称図形と点対称図形の見分け方 算数解法の極意
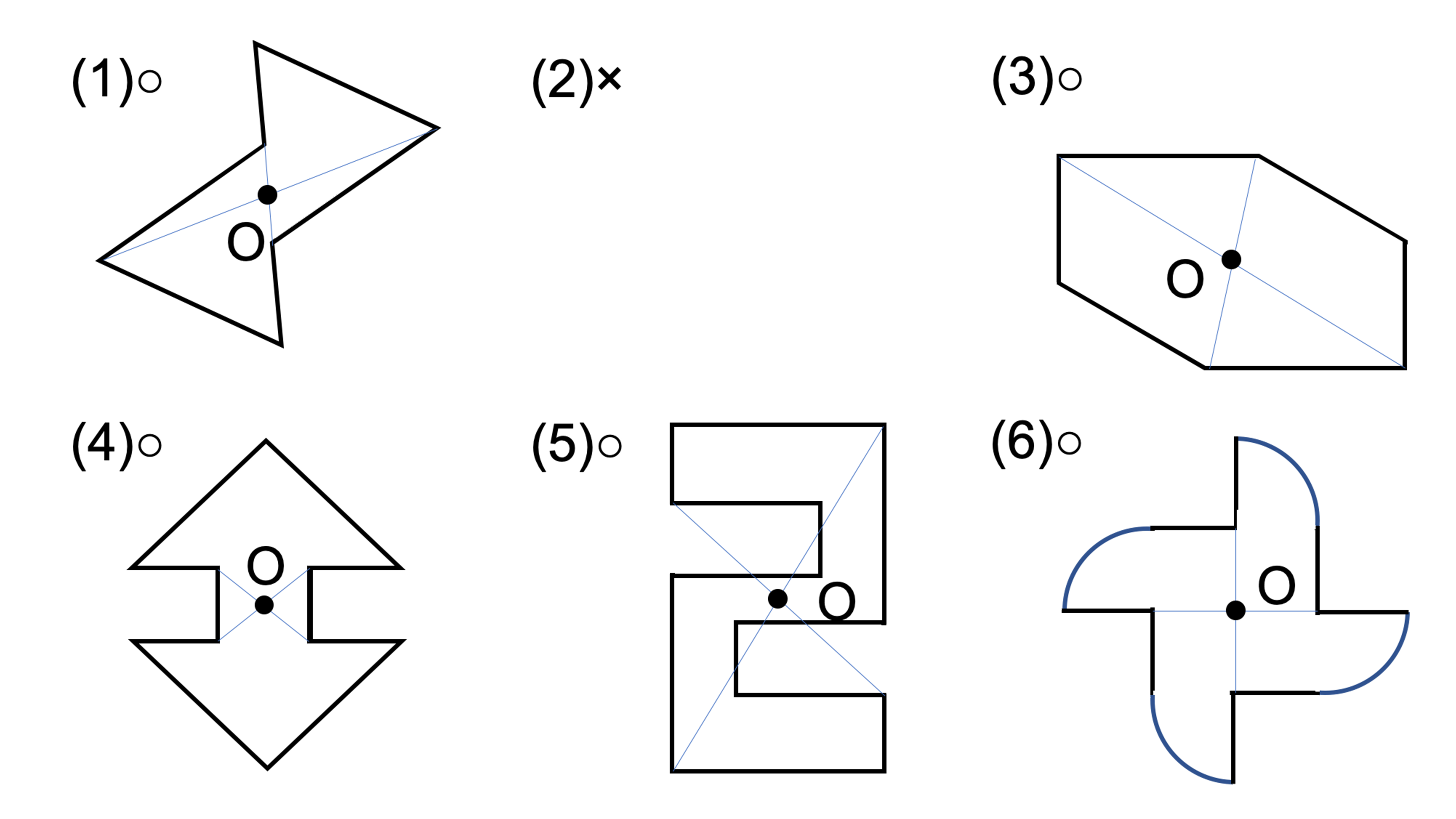
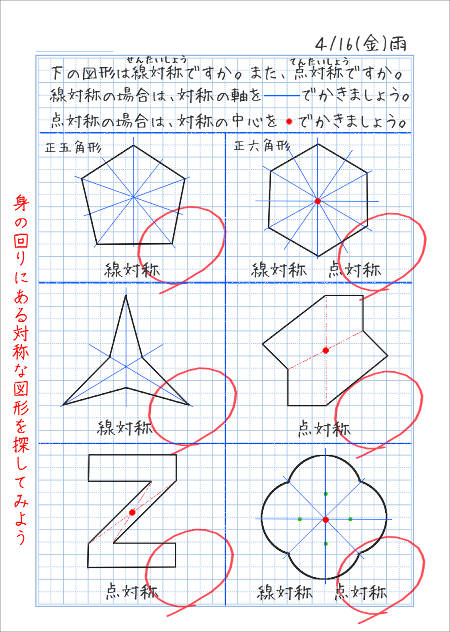
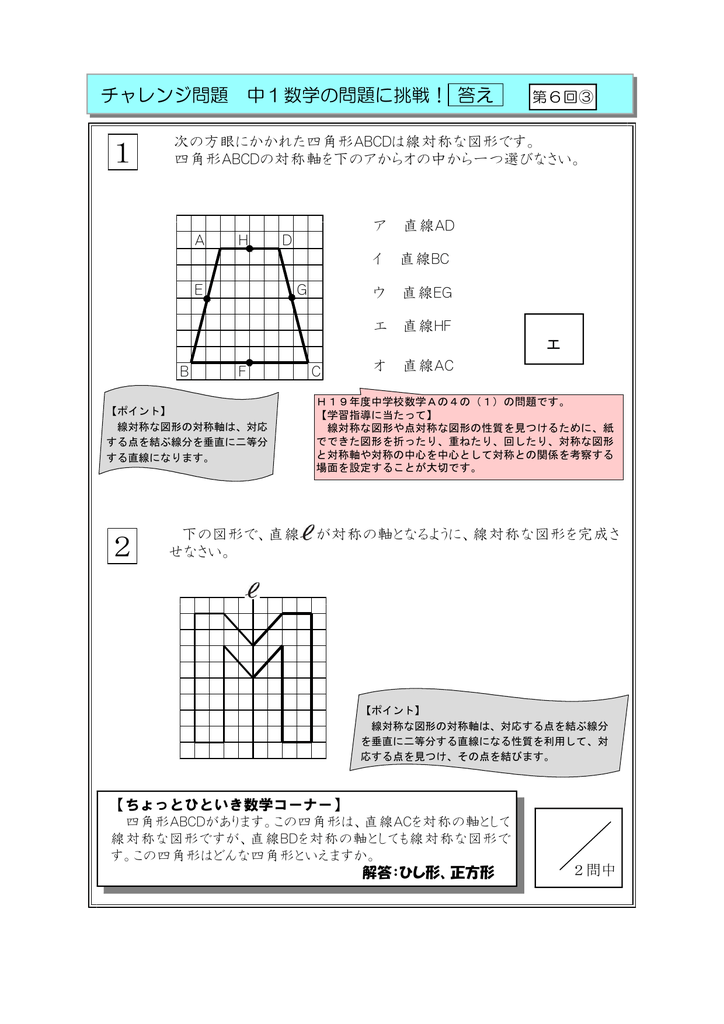
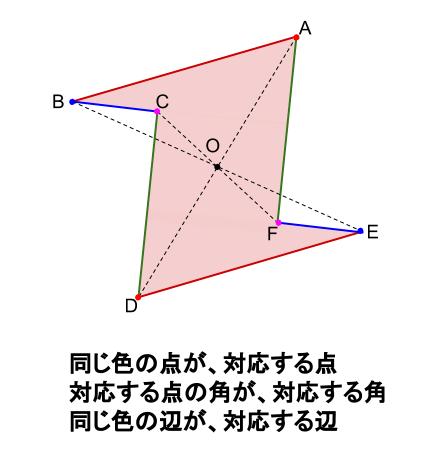
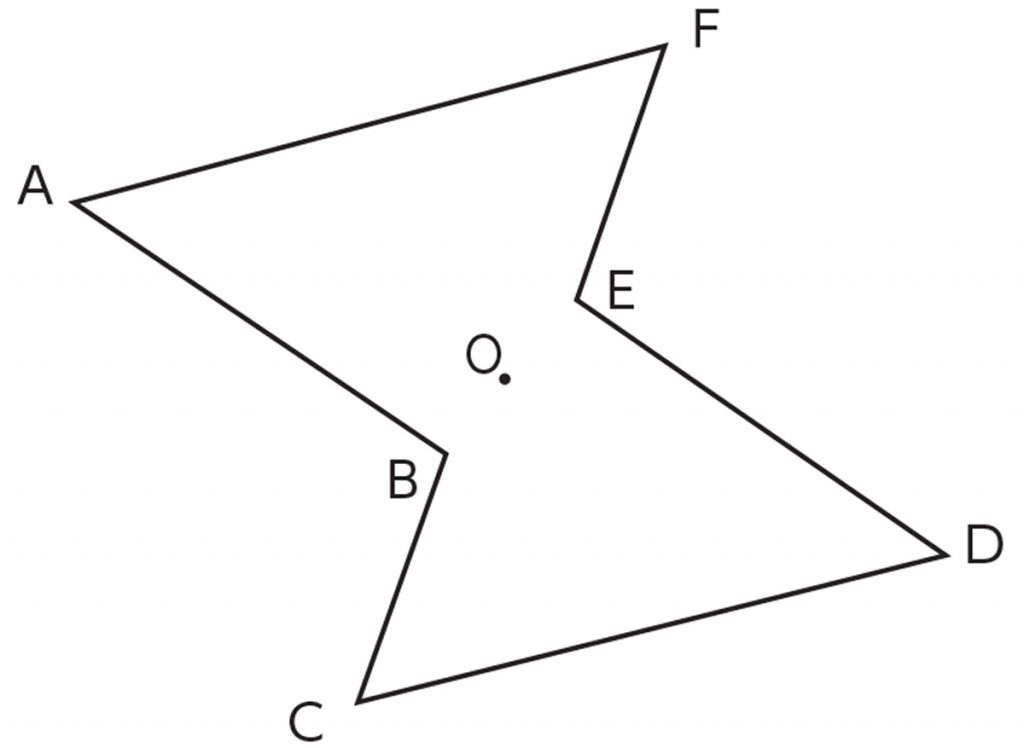
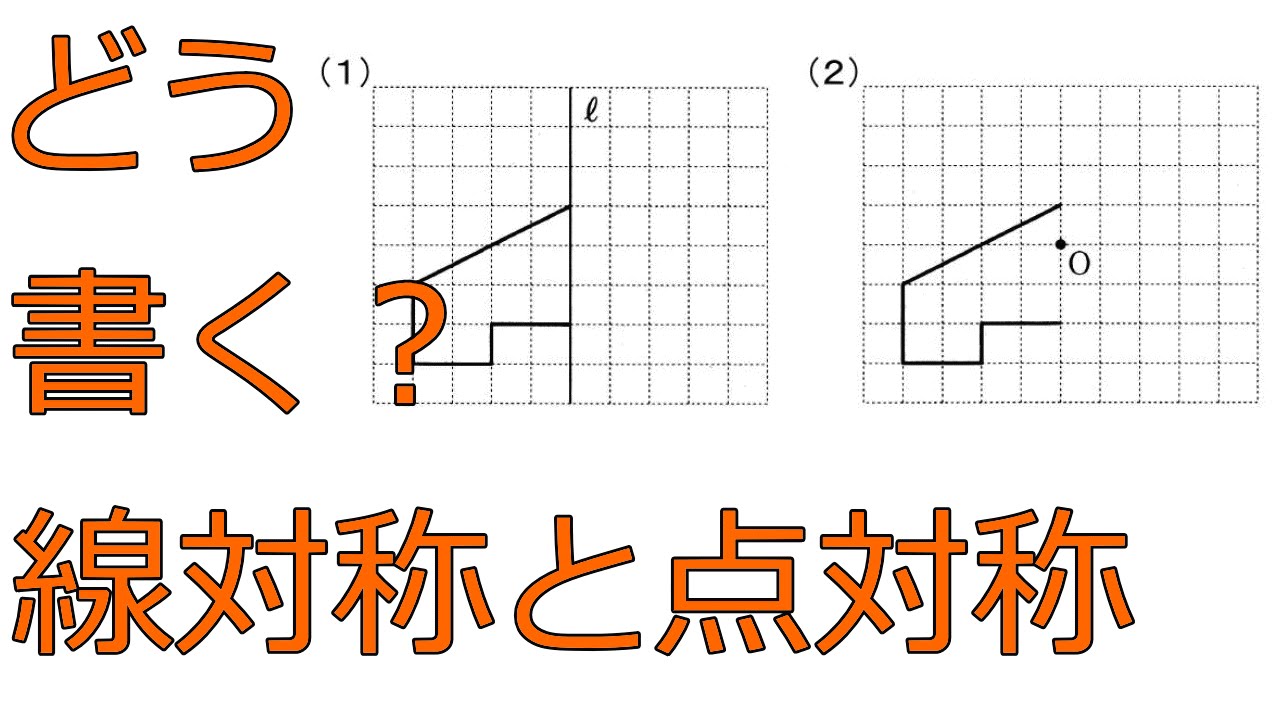
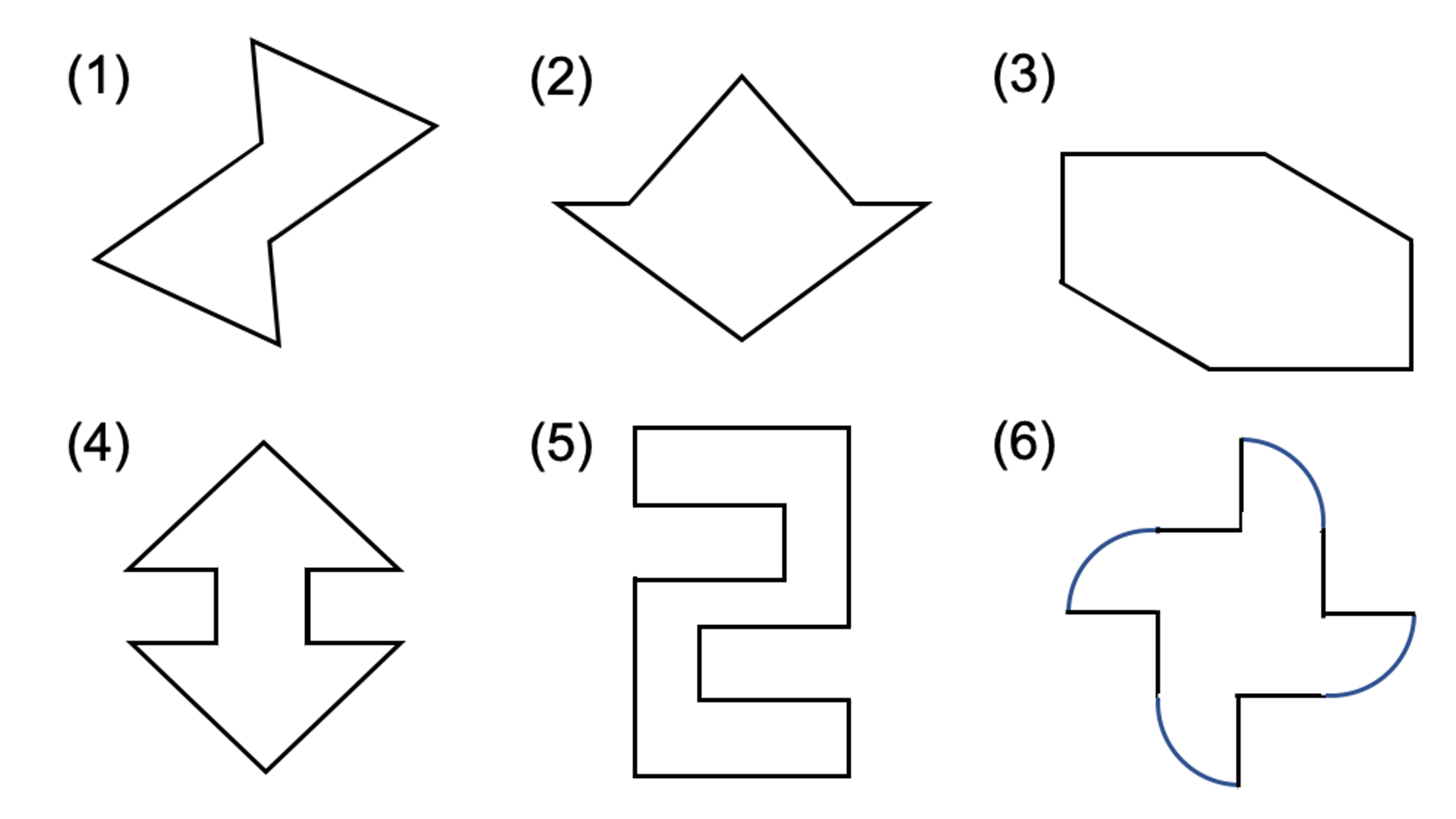
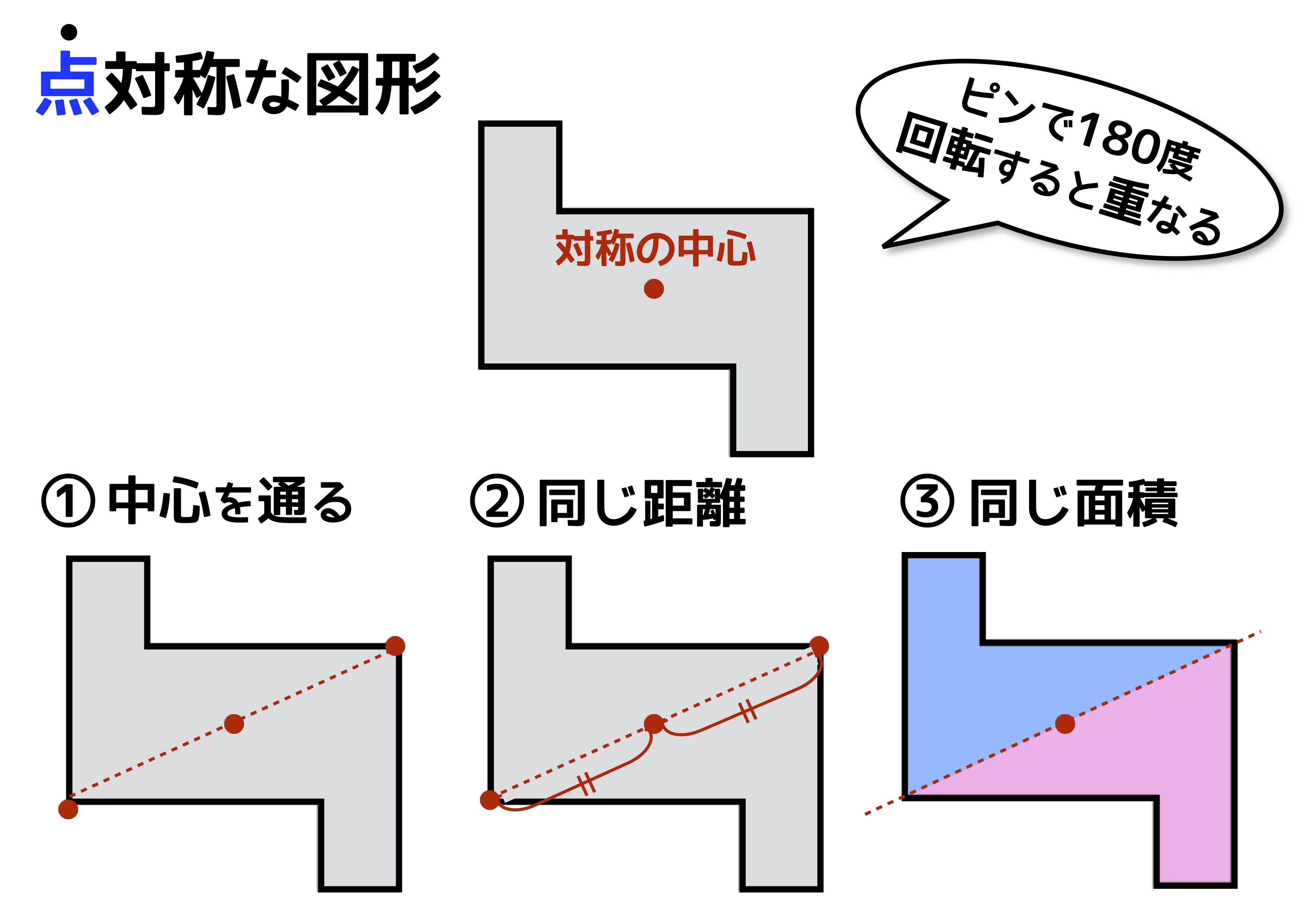
考える力を育てる 天才ドリル 平面図形が得意になる点描写 線対称小学校全学年用 算数 認知工学 本の購入は楽天ブックスで。全品送料無料!購入毎に「楽天ポイント」が貯まってお得!みんなのレビュー・感想も満載。 そして線対称と点対称の図形を見分ける問題はテストなどでよく聞かれます。 下の手順で見分けてみましょう。 ①図形に縦線を入れる ↓ ②図形を180度回転させる (①でできた、直線と図形の交点を上から下まで回して移動するイメージ) →180度回転させたときに元の図形と同じ形になれば「点対称」 →180度回転させる間に左右 この問題は与えられた図形が 「線対称である」 のか、 「点対称である」 のか、「 線対称であり、点対称である」 のか、 「どちらでもない」 のかの、 4つの選択肢から1つの解答を導く 問題と言えます。 線対称と点対称の定義は次のように与えられてい
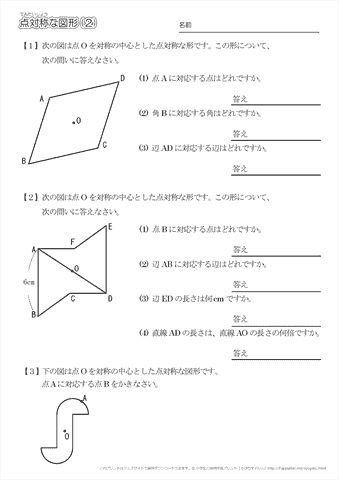
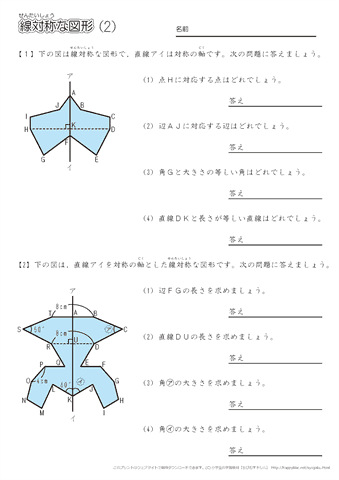
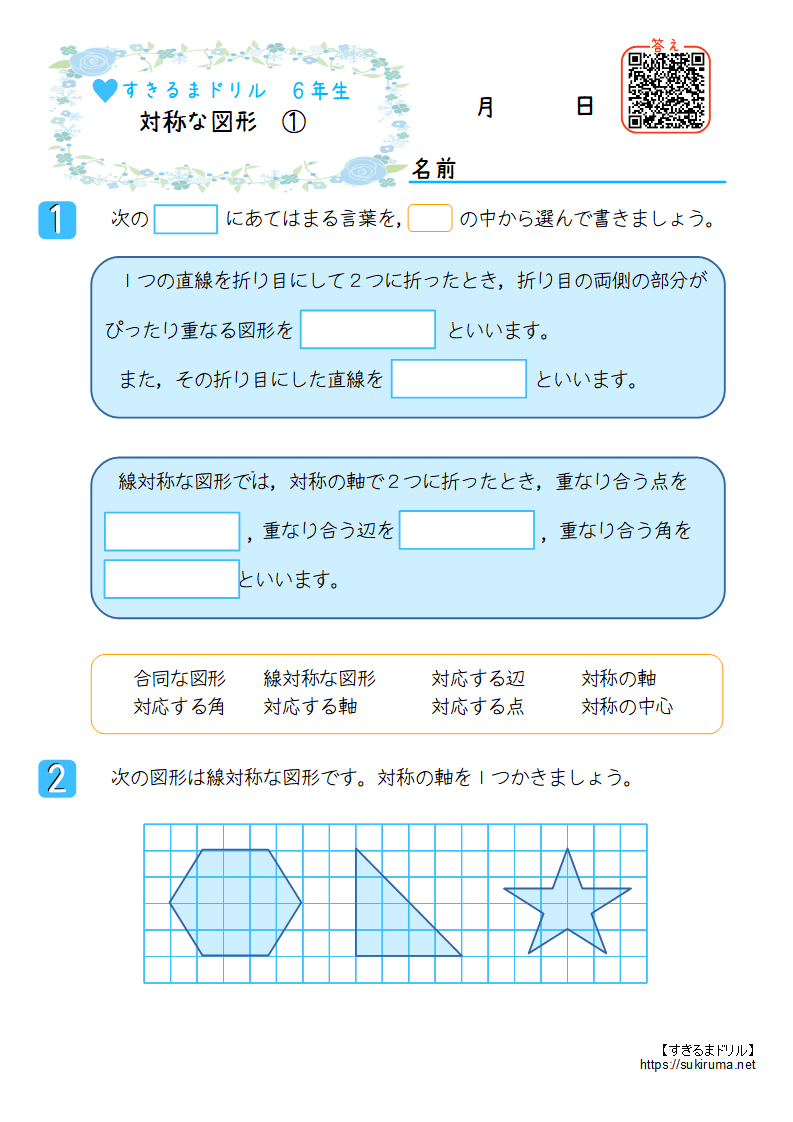
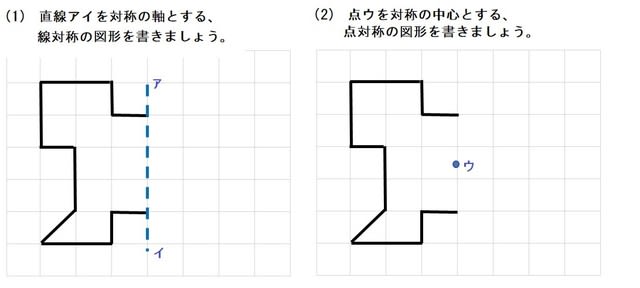
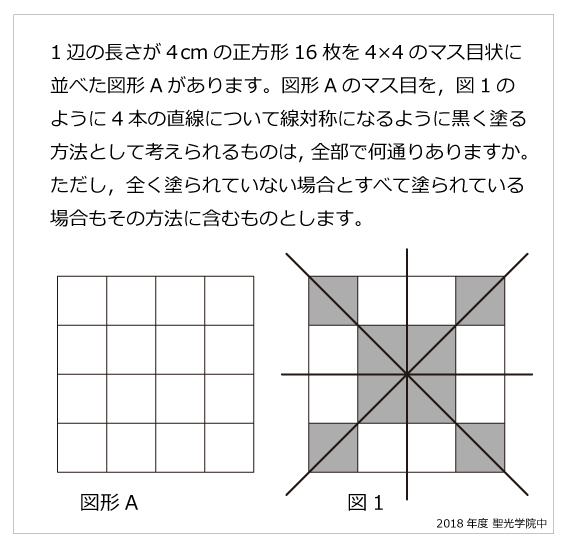
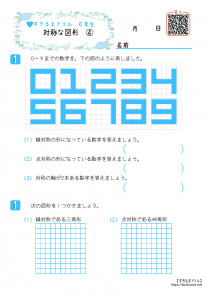
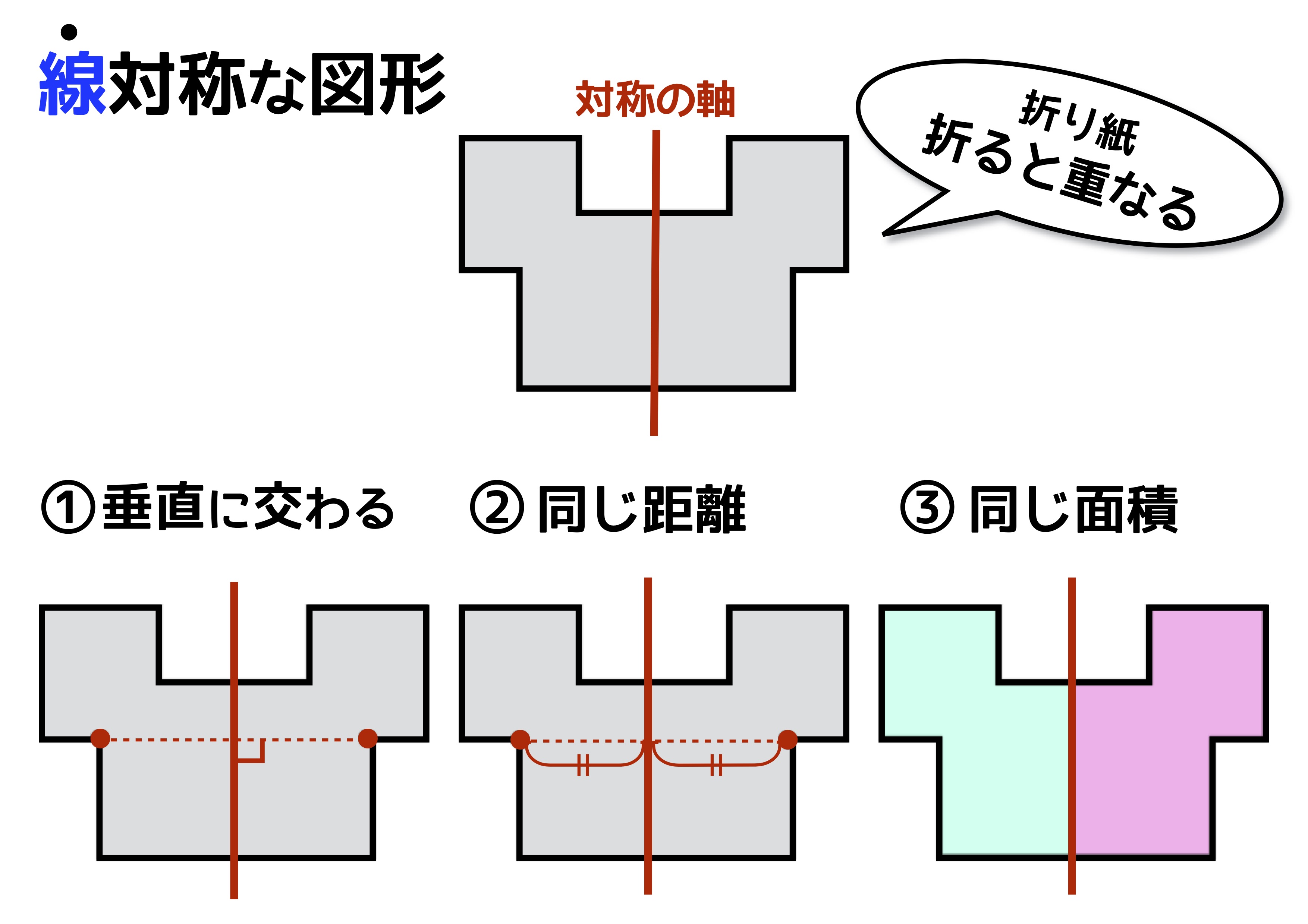
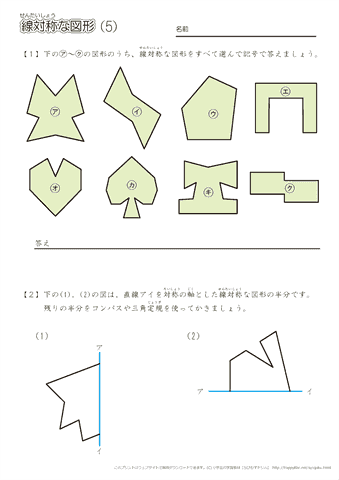
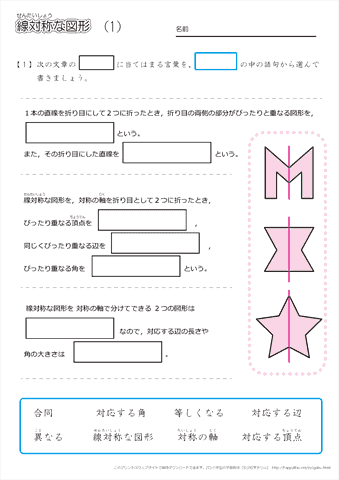
無料ダウンロード・印刷できる、線対称な図形の練習問題プリント です。 線対称な図形の意味と性質、図形さがし、作画などを練習し、理解を確かめることのできるプリントです。 線対称な図形(1) 答え 線対称な図形(2) 答え 線対称な図形(3) 答え 線対称な図形(4)小学6年生で習う、線対称な図形のかき方を練習できるプリントです。 作図が苦手なお子さんでも、色々な形の線対称な図形を練習することで、苦手意識をなくします。 「かんたん」「ふつう」「むずかしい」でプリントが分かれているため、学習進度によって選べます。 関連学習プリント 「線対称な図形の作図の練習問題」の講座と合わせて学習したいオススメ 小学校受験や日々思っていることを綴り始めて、100記事を突破しました。 お受験の問題は、就学前に身につけておいて欲しい内容なので、受験するしないに関わらず、チャレンジしてみるといいですよ。 意外に小学校、中学校の勉強にもつながっていたりします。 今回は、線対称の問題
線対称 点対称 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 | ||
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「線対称 点対称 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |
対称要素と点群 1 前回までの復習 入射X線 散乱X線 電子密度 位相差 e2Sir K 構造因子F 位相差を考慮して電子密 度を足し合わせたもの ³ 単位胞 FK Ure2SirKdV ³ 単位胞 F eihxkylzdV hkl Ur 2S 構造因子⇔電子密度 フーリエ級数 ¦¦¦ f f f f f f h k l ihxkylz Fhkle V Ur 1 2S i hkl Fhkl Fhkle M 位相問題 実験では座標がわかるときの対称点と直線の位置関係 点や直線が与えられた場合、 問題を解くとき真っ先にやることは位置関係をつかむための図を書くことです。 三角比や幾何ではもちろん、ベクトルや座標上に示せる点や直線や円の場合も簡単なものでもいいので書き出すことで解答の選択肢は増えますよ。 例題 直線 に関して点 と対称な点の座標 を求めよ。 これ





0 件のコメント:
コメントを投稿