中学受験Unit9 1 5年 立体図形1 体積と表面積 14 minsancom Title みんなの算数オンライン 中学受験5年Unit9 1 立体図形1 体積と表面積 Author みんなの算数オンライン Keywords 体積,表面積,単位換算,角柱,円柱,角錐,円錐,展開図中学受験の算数・理科ヘクトパスカルによる四谷大塚予習シリーズ算数「立体図形の研究(体積と表面積)の問題」の手書き解説です。立方体から直方体をいくつか取り除いて,右の図の ような立体を作りました。これについて,次の問いに 答えなさい。 (1) この立体の体積は何cm3ですか。1立方体と直方体 立方体の体積=1辺×1辺×1辺 立方体の表面積=1辺×1辺×6 直方体の体積=たて×よこ×高さ 2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい 角すいと円すいの体積=底面積×高さ×

小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすマンスリー 学習ポスター テストクイズ 3ステップ学習 算数 表面積 小学校 算数
立体の表面積と体積の求め方
立体の表面積と体積の求め方-空間図形(立体の表面積と体積) 学年 組 氏名 1 底面の半径が3㎝,母線の長さが6㎝の円錐です。この表面積を見取図と展開図をか いて求めなさい。求め方が分かるように,説明もかきなさい。 表面積を展開図を使って考える。 底面の円の面積は, 2)Hello School 算数 体積・表面積 練習問題 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 ※特に指定がない場合、円周率は314とします。




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
回転体の体積 下の図のような直角三角形abcで次のような二つの回転体をつくる。どちらの体積が大きいだろうか。 ア 直線abを軸として1回転させてできた立体 イ 直線acを軸として1回転させてできる立体 c b a 3㎝ 6㎝ c b a 3㎝ 6㎝ ア c a b 6㎝ 3㎝ イ 相似比と表面積と体積の関係 相似な図形が2つあり、相似比がa:bならば、表面積比は a²:b² 、体積比は a³:b³ になります。 注意:相似な図形である場合に限ります。 では問題です。 図のように三角錐O-ABCの底面ABCに平行な平面Lが、辺OAと点DでA = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径
表面積=4πr 2 、 体積= 4 3 πr 3 r (例)半径6cmの円 6cm 表面積=4π×6×6=144π (cm 2) 体積= 4 3 π×6×6×6=2π (cm 3)立体の体積&容積および諸数値 V=容積、S=表面積、As=側面積、Ab=底面積、x=底面より重心までの距離 寸 法 容積および諸数値 寸 法 容積および諸数値 V=a 2 S=6a 2 As=4d 2 正多角形 a=辺長表面積 = 2 × 半径 × 半径 × 314 直径 × 314 × 高さ
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして 立体の表面積を聞かれたら、展開図を書こう! ということ。展開図さえ書けば、そこに見えるのは長方形であったり、円であったり。ただの平面図形です。 それらの面積を1つ1つ出してから足し合わせるだけ。シンプルです。 立体の体積 表面積の後は数学16章空間図形「立体の表面積と体積」<基本問題②・解答> 1 解説 (1)体積 384㎝3 (表面積384㎝2 (2)体積96π㎝3 (表面積96π㎝ (3)体積36π㎝3 (表面積36π㎝π=36π 2 解説 ㎝3 展開図を組み立てると,



6 13 第6章 空間図形立体の表面積と体積 角柱や円柱の体積 ニュージーランド短期留学ダイアリー



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー
・立体の表面積や体積を求める公式を進んで活用しようとする。 ・直方体の体積の求め方と関連づけて、角柱や円柱の体積の求め方を考えたり、 実 験や実測によって錐体の体積の求め方を工夫できる。体積 = 底面積 × 高さ ÷ 3立体の体積、表面積 問題 ・・・ (む) は難しい問題です。 1 右図の四角錐の底面は1辺の長さ6 (cm)の正方形,側面は等しい辺の長さが2√7 (cm)の二等辺三角形です。 この四角錐の体積は (cm 3 ) ア= イ= この四角錐の表面積は (cm2) ウ= エ= オ= 2 右図は1辺の




表面積の求め方 計算公式一覧




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
立体全体の表面全体の面積を表面積という。 ① 角柱・円柱の表面積 底面積 側面 ② 角柱・円柱の表面積 底面の周の長さ 高さ ③ 角柱・円柱の体積 底面積 高さ 例)3辺の長さが の直方体がある。 この直方体の表面積と体積を求める。 表面積 底面積 側立体の表面積と体積 1立体の表面積 ポイント:面積の意味,単位が理解できる 広さのことを面積といいます。 1辺が1cmの正方形の面積を 1c㎡(1平方センチメートル)といいます。 1cm2の正方形が5個あるので、5cm2となります。立体の表面積 → 携帯版は別頁 == 立体の表面積展開図(入試問題) == 要点11 ≪円柱の側面積≫ 円柱の表面積は,2つの底面積と側面積の和になります. 右図のように底面の半径が r ,高さが h である円柱の側面は長方形で,側面積は 2πr×h になります. ※以下に引用している入試問題で,元の問題は記述式ですが,この教材ではWeb上での操作性をよくする




立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット




角錐 円錐の体積と表面積の公式 数学fun
表面積や体積の求め方 (三角柱,四角柱,円柱,球や半球) 表面積や体積の求め方のポイントです。 代表的な三角柱,四角柱,円柱,球や半球などを取り上げて説明しますが、公式ではなく、求めるための手順を覚えるようにしましょう。 問題には公式が使えない立体が多く出てきますので、覚えることを間違えないようにしてください。立体図形の切り口(浦和明の星中学 受験算数問題 09年) 立体の表面積と体積(中学受験 算数入試問題) 重なった三角柱(中学受験算数 立体図形) 表面積と体積は? (中学受験算数 頭の中で回してみた問) 面積の差は? (中学受験算数 難しく考え小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題




Sqrt8 Y Descubre Como Resolverlo En Qanda



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com
2/3時 ・ 相似な立体について、相似比と表面積の比、体積の比の関係を考察することができる。 本時の学習内容「立体の表面積や体積を、相似比と表面積の比、体積の比の関係を調べよう」を知る。 教科書133ページの「ひろげよう」を考える。 直方体楕円体の体積 腎臓の大まかな体積の確認目的。 楕円体形状の腎臓動脈瘤の塞栓で、使用するコイルの適合サイズを表面積で推測するのに使用しました。 大変役に立ちました。 ありがとうございました。 学校の宿題に使いました。 ありがとうござい立体のすべての面の面積の和を( 表面積 )という。また、側面全体の面積を ( 側面積 )、 1つの底面の面積を( 底面積 )という。 2 次の立体について、表面積と体積をそれぞれ求めなさい




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ
これを具体的に説明してみようと思います。 まず、頭の中に1辺が1センチのサイコロを1つ思い浮かべてみて下さい。 そのサイコロの体積は、もちろん「1立方センチメートル」ですよね。 面積は、というと、6つの面があるのですから、「6平方センチメートル」です。 単位がついていると面倒なので、単位を除くと、 体積1 : 表面積6 ということですね。 ではつかむ 本時の学習内容「角柱や円柱の体積の求め方を考えよう」を知る。 教科書177ページの「ふりかえり」に取り組む。 「直方体の体積」=「縦」×「横」×「高さ」 =「底面積」×「高さ」 を確認する。 課題を考える。 右の図のような、直方体を2つに切った三角柱があります。 この三角柱の体積を求めなさい。 積み重ねられた立体の体積:立体を段ごとに分解 最初は自分で図を描いてみても良いです。 125 260 180+108+45=333 125+260+333=125+593=718 答え)718cm 3 (2)この立体の表面積を求めなさい 積み重ねられた立体の表面積:(前+右+上)×2 97+97+111
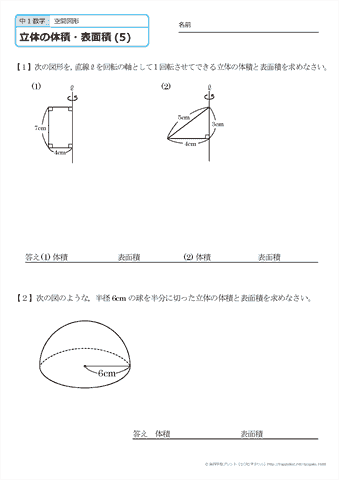



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 中1 数学まとめ 立体の体積や表面積など 中学生 数学のノート Clear
立方体の辺の長さから体積と表面積を計算します。 立方体の辺の長さ 立方体の辺の長さ 立方体の体積から辺の長さと表面積を計算します。 直方体の体積 直方体の体積 直方体の三辺の長さから体積と表面積を計算します。 四面体の体積 四面体の体積面積 メンガーのスポンジの次元は2より大きいため、2次元的な大きさである 面積 は無限である。 表面積が1となる大きな立方体から穴を空けてメンガーのスポンジを構成する場合、一度目の穴を空けると、その表面積は 1 3 {\displaystyle {\tfrac {1}{3}}} 増加する。一番大きいと思う立体を、各自で作る。 展開図を準備しておく) グループで城の大きさ比べをする。 分解した立体で形を整理する。 分類(柱体・すい体)して、求め方を考える。 1)表面積では 2)体積



高校入試 英語 数学 学習 立体の表面積と体積




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学
体積・表面積 算数 中学数学 空間図形 立体の 体積の求め方(公式) を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め① 立体のすべての面の面積の和を表面積という。 また,側面全体の面積を側面積,1 つの底面の 面積を底面積という。 ②(柱体の体積)=(底面積)×(高さ),(柱体の表面積)=(側面積)+(底面In 平面図形 おもしろ算数問題(面積を求める)|久留米大学附設中学校 Home » 単元別の研究 » 図形に関する問題 » 立体図形 » 体積と表面積の問題3|考え方と解き方



立体 の 表面積 求め 方




中3 三年数学 立体の表面積の比と体積の比 中学生 数学のノート Clear
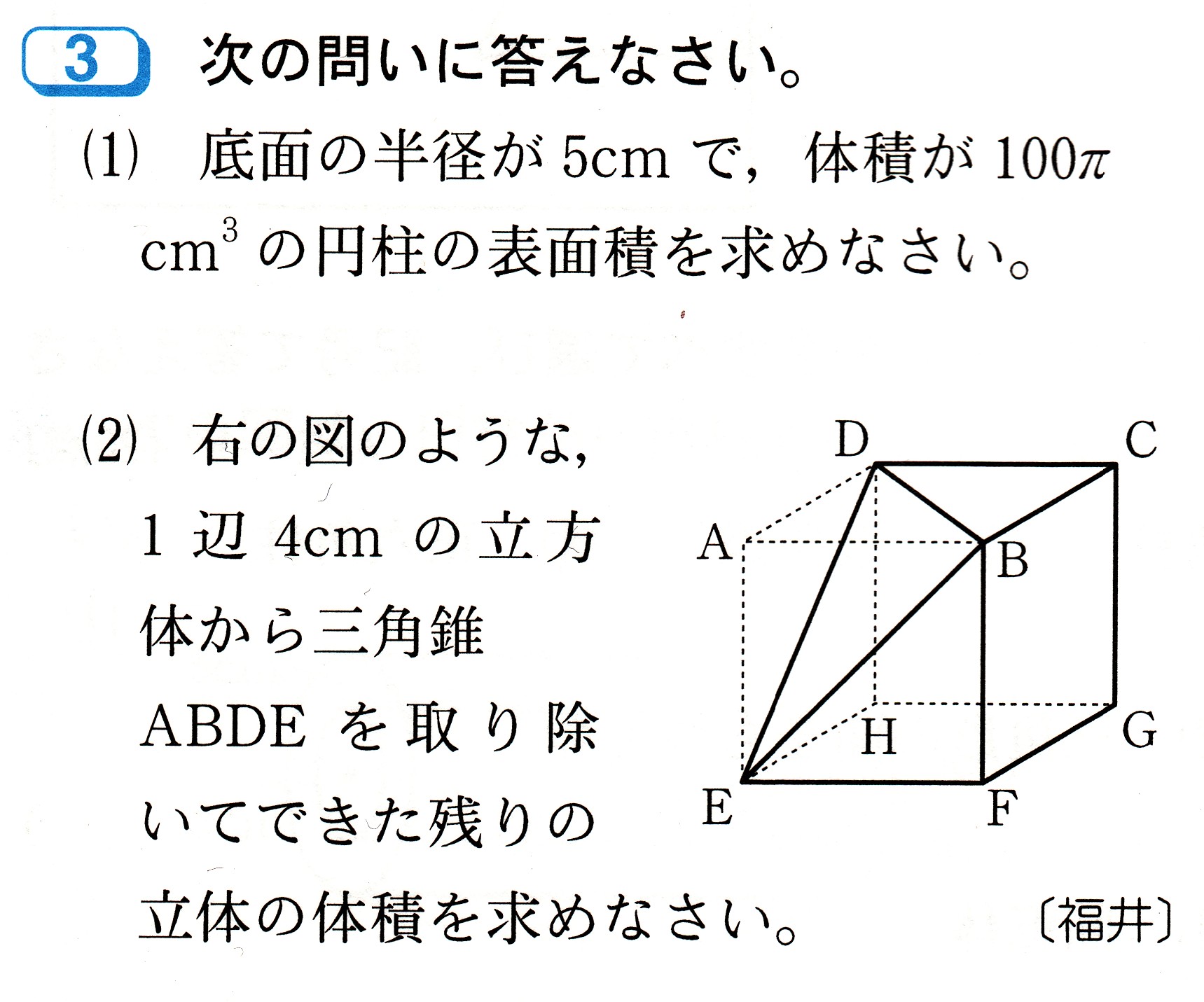



中学1年数学 立体の表面積と体積 確認問題3 あんのん塾
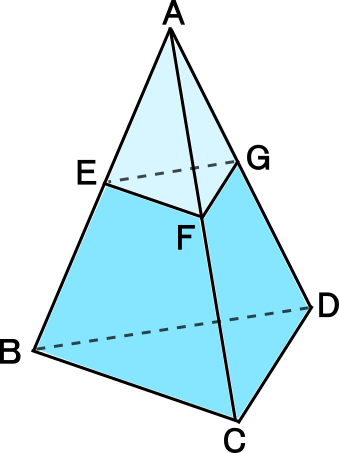



中学3年数学練習問題 相似な立体の表面積と体積の比 図形と相似



1




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム



中学1年数学 立体の表面積と体積 確認問題6 あんのん塾




立体の表面積と体積 数学の要点まとめ 練習問題一覧
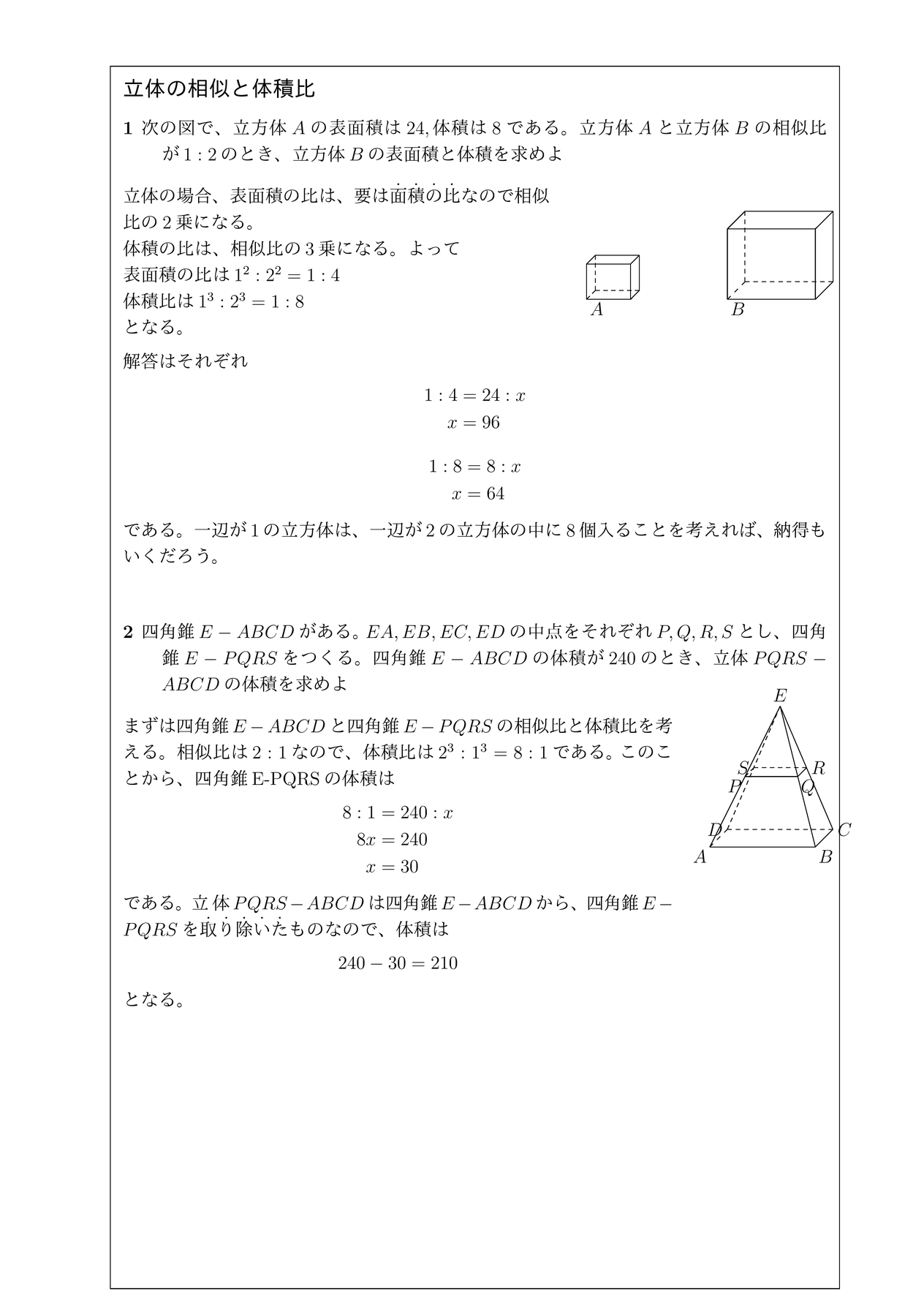



立体の相似と表面積比 体積比 チーム エン




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




表面積の求め方 計算公式一覧



1




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



1
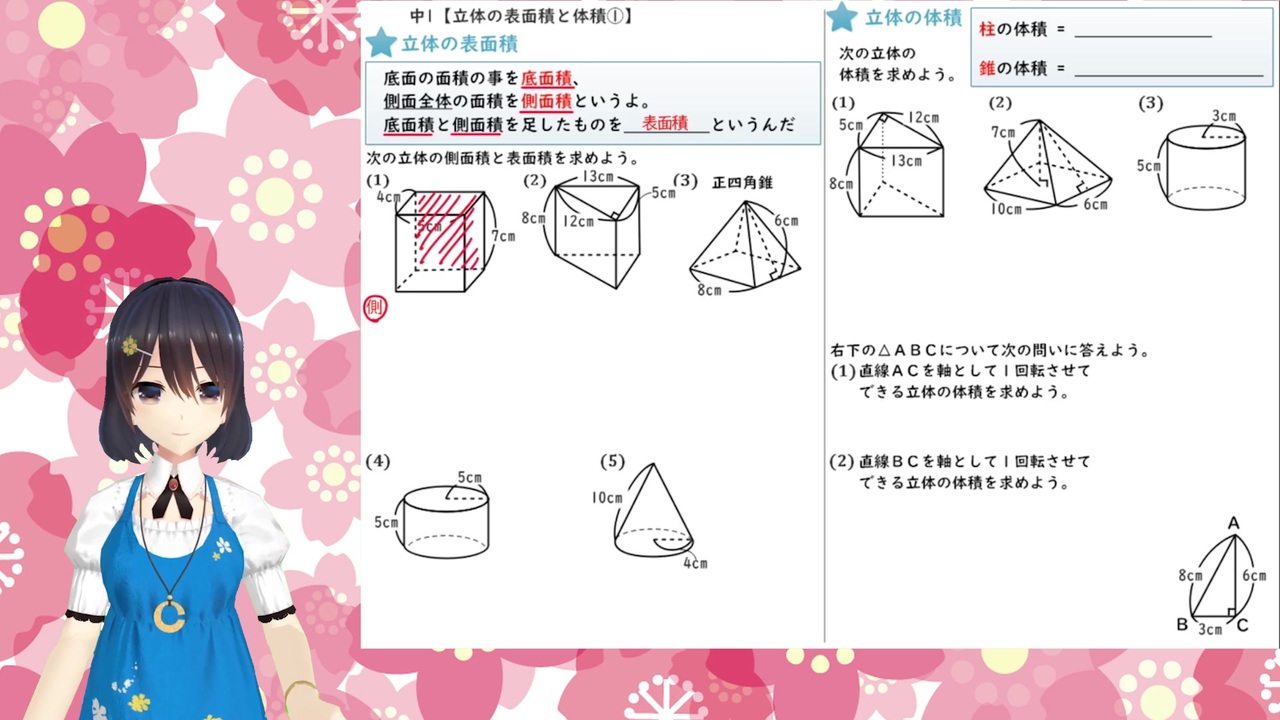



数学 中学1年 立体の表面積と体積 ニコニコ動画




球の体積と表面積 公式と計算問題と証明 Irohabook
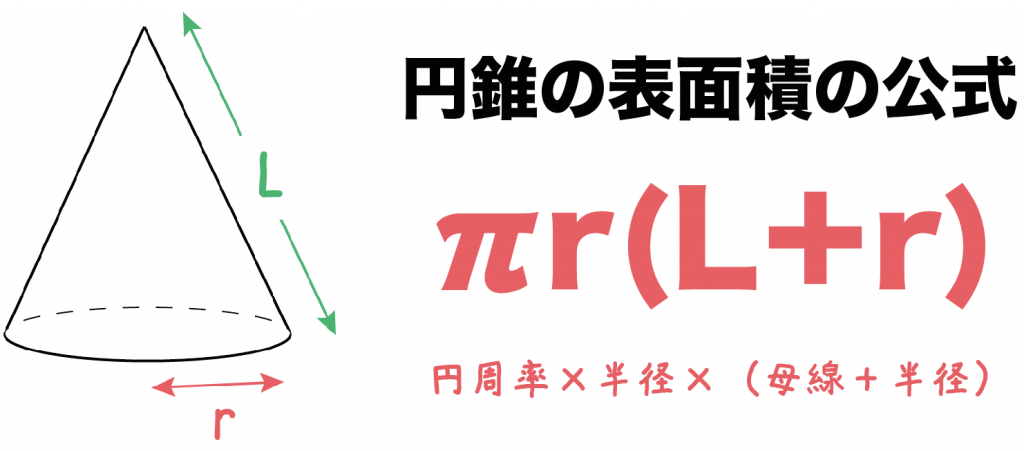



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題




中1 数学 中1 立体の体積 Youtube



中1数学 立体の表面積と体積の求め方と練習問題 Pikuu



1
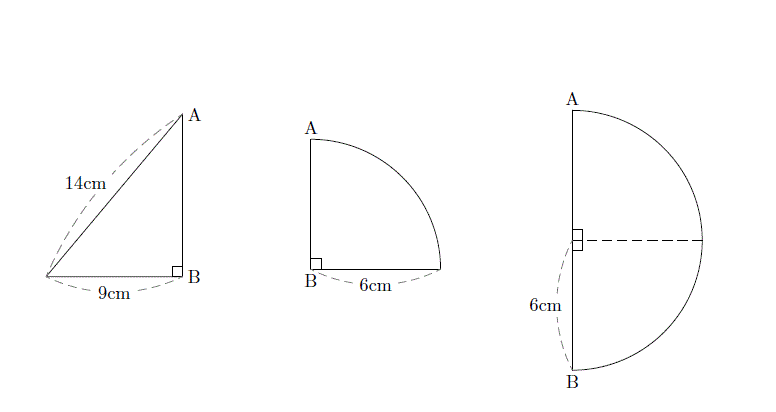



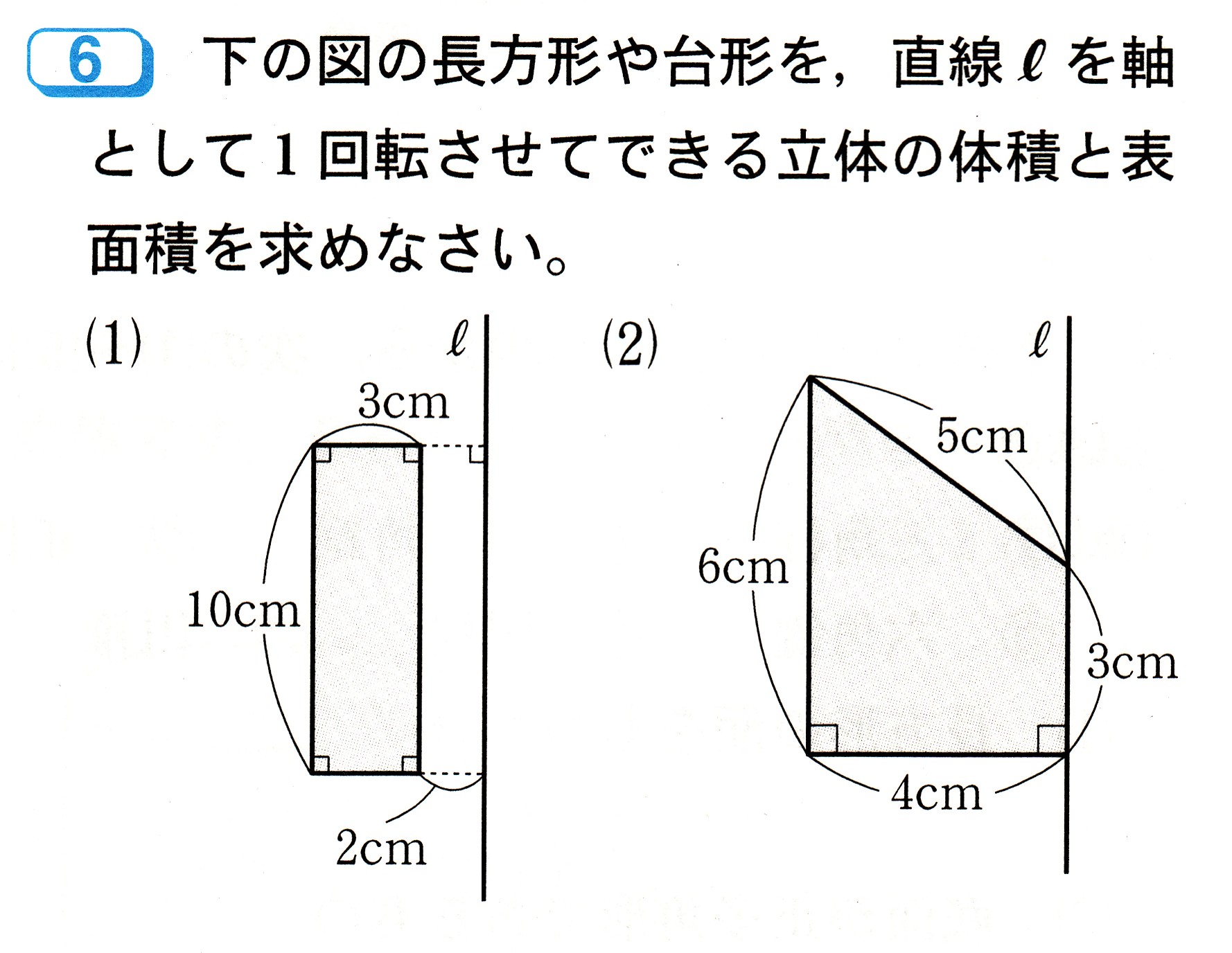
かみのドリル 立体の体積と表面積 回転




公式を図解 すい体の体積 円すいの表面積の求め方




角柱 円柱の表面積と体積の公式 数学fun




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear




角錐 円錐の体積と表面積の公式 数学fun
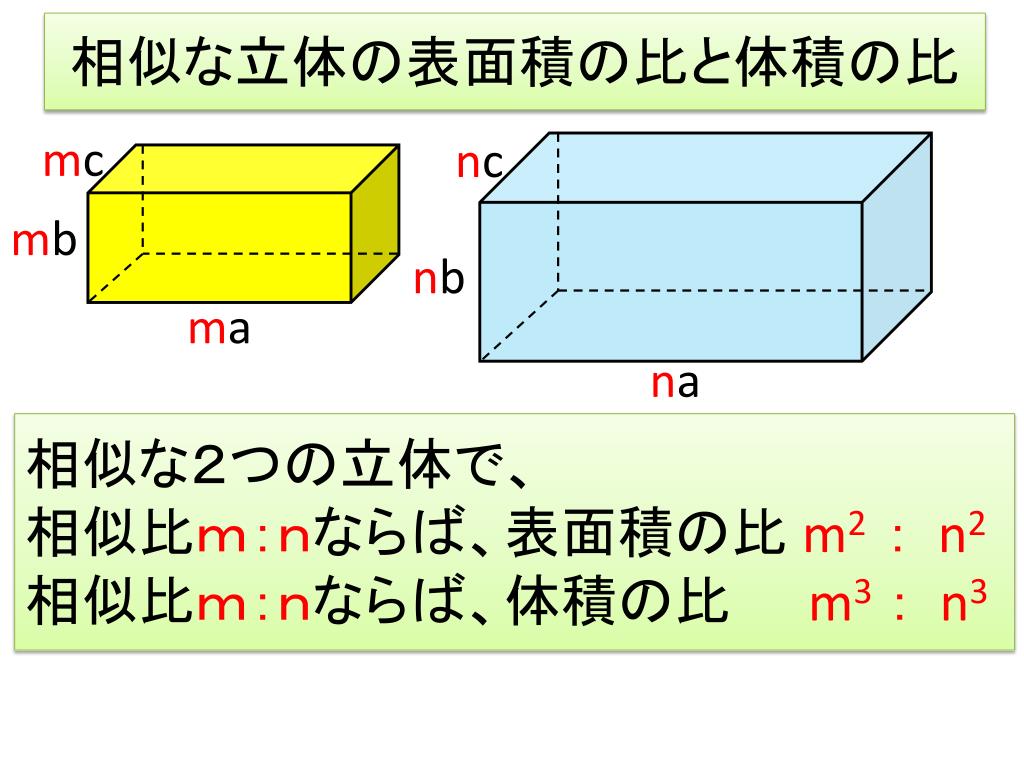



Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id




中1 数学 6 5 球の体積 表面積 Youtube



6 3 複雑な図形を1回転させてできる立体の体積と表面積を求めるには さんすうがく パート 2
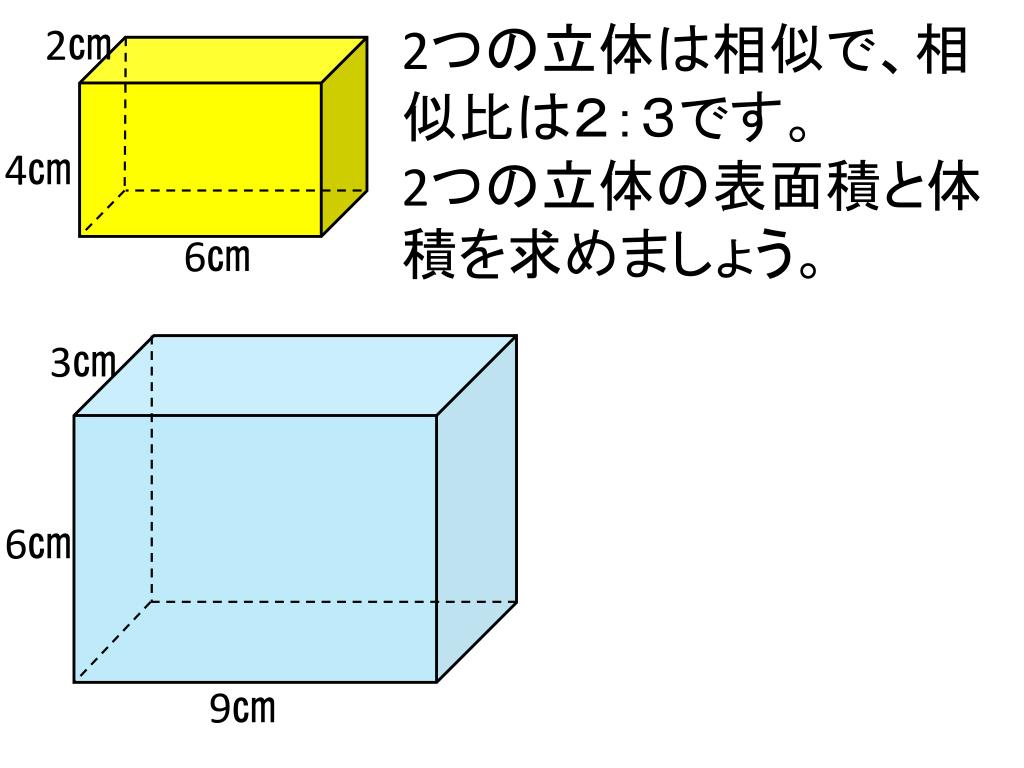



Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




球の表面積と体積の公式 数学fun
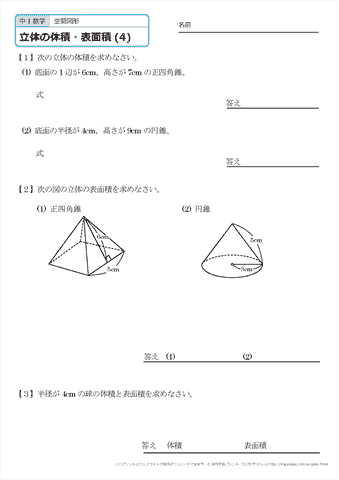



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 中1数学 空間図形 体積と表面積の公式一覧 中学生 数学のノート Clear



無料 中1数学 基本問題 問題プリント 空間図形6 立体の体積 143



立体の表面積と体積 わかる数学
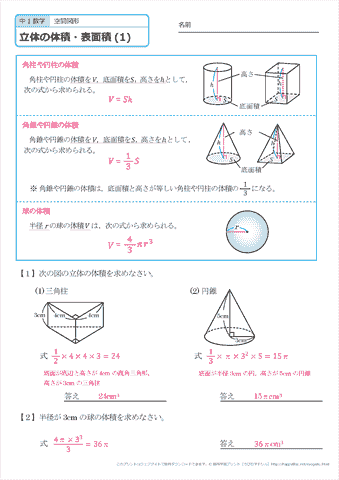



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく



高校入試 英語 数学 学習 立体の表面積と体積




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




本時の目標 身近な直方体をもとに実際に表面積と体積を求めることで 相似な立体の表面積比と体積比について理解する Ppt Download




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com



5 5 複雑な立体の表面積と面積を求めるには さんすうがく
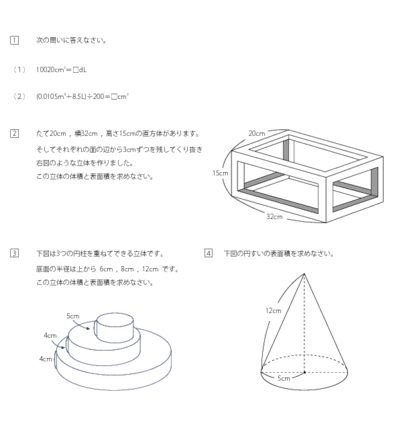



みんなの算数オンライン 中学受験5年 立体図形1 体積と表面積
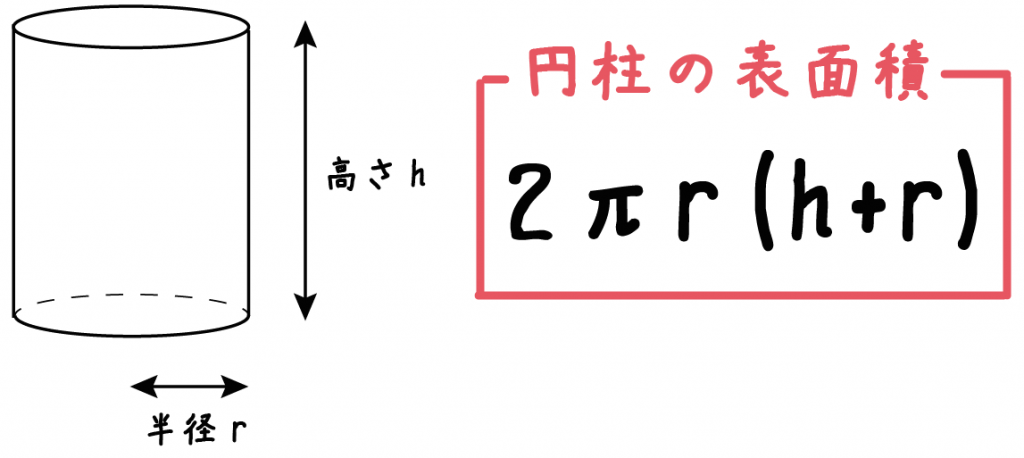



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
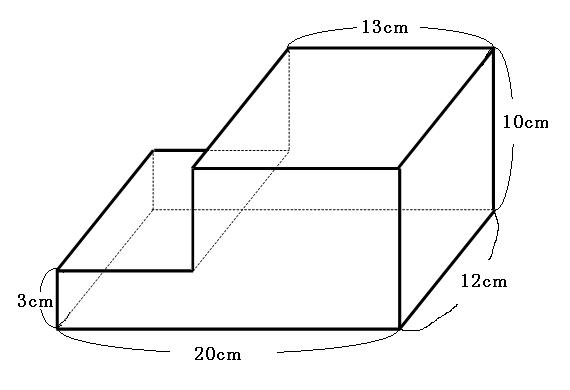



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか



立体の表面積と体積 わかる数学




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu
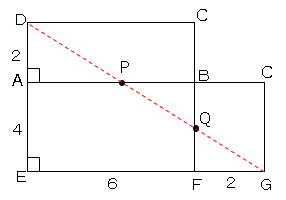



立体の表面積と体積50 数学の要点まとめ 練習問題一覧




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすマンスリー 学習ポスター テストクイズ 3ステップ学習 算数 表面積 小学校 算数




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



無料 中1数学 標準問題 解答プリント 143 空間図形6 立体の体積




Sqrt5 L 1 L Descubre Como Resolverlo En Qanda




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




5章3節2 相似な立体の表面積や体積の比 数学のすすめ



この問図形の表面積と体積を教えてください 上の円錐と円柱 Yahoo 知恵袋



立体 の 表面積 求め 方
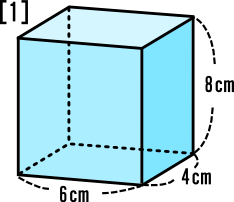



中学1年数学練習問題 立体 円柱 三角柱 四角錘等 の表面積の問題
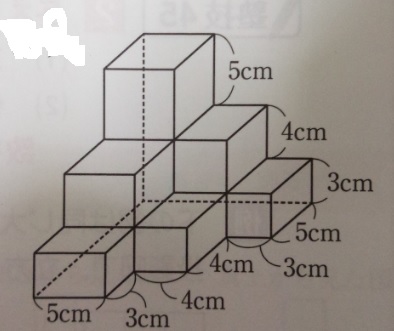



積み重ねられた立体 表面積と体積 中学受験 塾なし の勉強法




公式を図解 すい体の体積 円すいの表面積の求め方




5 Descubre Como Resolverlo En Qanda




複雑な体積 表面積の問題 家庭教師としの勉強部屋
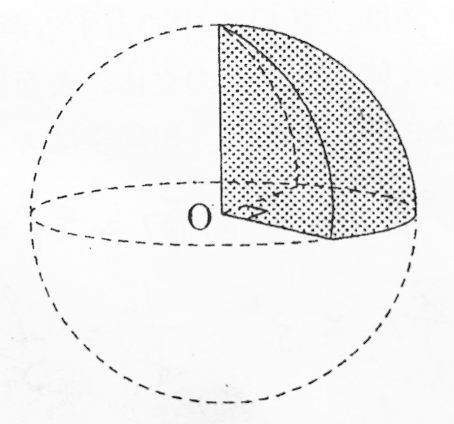



球の問題 苦手な数学を簡単に
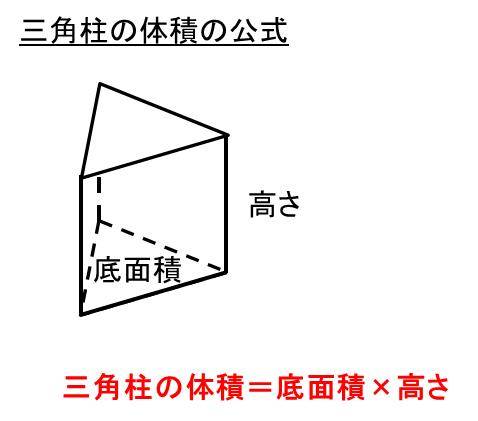



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム
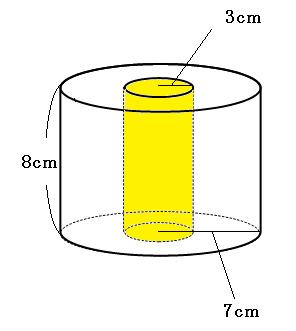



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com



立体の表面積と体積 中学受験 算数入試問題 どう解く 中学受験算数




立体の表面積と体積 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




球の表面積と体積の公式 数学fun




10 面積比 体積比 球の表面積と体積




5章3節2 相似な立体の表面積や体積の比 数学のすすめ



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor



立体の表面積




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




角柱 円柱の表面積と体積の公式 数学fun




体積 表面積




Ppt 相似な立体の表面積 体積 Powerpoint Presentation Free Download Id



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋
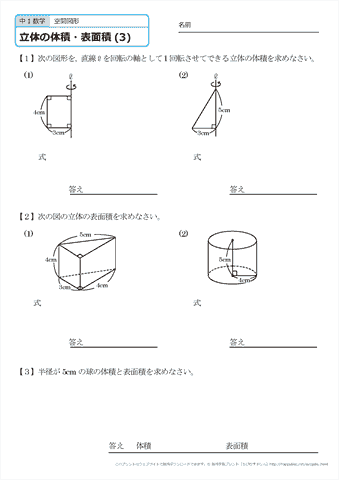



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




円錐の表面積 Youtube




中1数学31 立体の表面積と体積 Youtube




中1 数学 中1 立体の表面積 Youtube




立体の表面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット



立体の表面積




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




1 Descubre Como Resolverlo En Qanda



0 件のコメント:
コメントを投稿